Зубова С.П., кандидат педагогических наук, доцент ФГБОУ ВО СГСПУ, Самара
Зубова С.П., кандидат педагогических наук, доцент ФГБОУ ВО СГСПУ, Самара
E-mail: zubova@pgsga.ru
Лысогорова Л.В., кандидат педагогических наук, доцент ФГБОУ ВО СГСПУ, Самара
E-mail: lysogorova@pgsga.ru
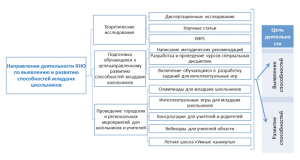
В статье рассматривается система, направленная на выявление и развитие способностей младших школьников. Работа, организованная кафедрой начального образования, осуществляется по нескольким направлениям: теоретические исследования, просвещённые проблеме исследования; подготовка студентов к целенаправленному развитию способностей младших школьников: организация и проведение городских и региональных мероприятий для школьников и учителей, на которых осуществляется показ направлений и перспективы развития математических способностей младших школьников в обучении математике.
The article considers a system aimed at identifying and developing the abilities of younger schoolchildren. The work organized by the Department of Primary Education is carried out in several directions: theoretical research, enlightened research; preparation of students for the purposeful development of the abilities of younger schoolchildren: organization and holding of urban and regional events for schoolchildren and teachers, which show the directions and prospects for the development of mathematical abilities of younger schoolchildren in teaching mathematics.
В первую очередь, хотелось бы отметить, что проблема развития способностей младших школьников в последнее время все чаще выносится «за кадр», уступая место «грамотностям» — функциональной, ее составляющим – математической, читательской, финансовой и так далее. Межу тем, в компетентностно-ориентированном подходе образовательные результаты трактуются как способности или готовности к определенного вида деятельности. То есть получается, что компетенции как способности в своем развитии и формировании проходят путь от способностей как природных задатков к способностям развитым, включающим в себя, кроме природных задатков, еще и приобретенные знания, умения, ценностные установки, личностные качества и опыт деятельности. В сказанном ключевым является слово «приобретенные». Это означает, что без специальной организации образовательного процесса, направленной на развитие способностей они так, и останутся просто задатками, не реализованными в жизни индивидуума.
Отсюда мы видим важность исследования природы способностей и поиска путей их развития. Как основа компетенций способности целесообразно начинать развивать уже с дошкольного возраста.
Понятно, что исследование проблемы нужно начинать с ее теоретического осмысления для выстраивания траектории ее решения. Поэтому на кафедре начального образования осуществляется поиск новых способов развития способностей младших школьников и обучающихся вузов, результаты этого поиска представляются в диссертациях, выпускных квалификационных работах, публикуются в научных статьях.
Для подготовки обучающихся нашего факультета изданы методические рекомендации, которые используются при изучении методических дисциплин.
Поскольку способности – это качества личности, в определении этого понятия уместен личностно-ориентированный подход. при таком подходе способности трактуются как индивидуально-психологические особенности личности, обеспечивающие успех в деятельности, в общении и легкость овладения ими. Способности не могут быть сведены к знаниям, умениям и навыкам, имеющимся у человека, но способности обеспечивают их наиболее быстрое приобретение.
Такое понимание способностей совпадает с точкой зрения Б.М. Теплова. В понятие способность он включал три признака: во-первых, под способностями подразумеваются индивидуально-психологические особенности, отличающие одного человека от другого; во-вторых, способностями называют не всякие вообще индивидуальные особенности, а лишь такие, которые имеют отношение к успешности выполнения какой-либо деятельности; в-третьих, понятие способности не сводится к знаниям, умениям, навыкам, которые уже выработаны у данного человека.
Что нам дает такая трактовка: во-первых, понимание того, что нельзя обучение сводить только к передаче знаний и отработке умений, что, к сожалению, мы сейчас часто можем наблюдать на практике; во-вторых, владение развитыми способностями является определяющим фактором успешности в дальнейшей жизни, дающим возможность в быстро изменяющихся условиях быстро и легко приобретать новые знания, овладевать новыми способами действий, следовательно, возникает насущная необходимость направить обучение на развитие способностей, а значит, перестраивать кардинально сам процесс обучения. В-третьих, способности – это индивидуальные качества и для успешного их развития требуется понимать их сущность и структуру. В настоящее время выделено много разных видов способностей. Понятно, что сразу все способности развивать у школьников невозможно, поэтому желательно, с одной стороны, направить обучение на развитие общих способностей, а с другой стороны, определить склонности каждого ребенка и уже на основе развитых общих способностей развивать специальные. Так, например, целесообразно развивать гибкость мышления как общую способность, а на математическом содержании эта способность будет проявляться как умение находить разные способы решения математических задач.
К сожалению, несмотря на то, что в последнее время учебники математики стали содержать большее количество так называемых занимательных задач, приходится констатировать, что далеко не все учителя начальных классов понимают, на формирование какого компонента способностей направлено то или иное задание, действуют часто интуитивно, не видят перспективы развития способностей, что негативно влияет на качество обучения и развития.
Традиционными стали математические олимпиады для школ города и области, содержание которых разрабатывается на кафедре начального образования. Целью их проведения является не только выявление математически способных детей, но и показ направлений и перспективы развития математических способностей младших школьников в обучении математике.[1] Школьники, участвующие в олимпиадах, получают задания и затем, после участия, анализируют их выполнение вместе со своим учителем. Во время проведения олимпиады преподаватели кафедры проводят консультации с учителями и родителями, сопровождающими школьников, где подробно рассказывают, какие способности или какие компоненты способностей должны проявить участники олимпиады для успешного выполнения конкретных заданий.
В процессе проверки диагностическая направленность заданий разъяснялась учителям. В заданиях была заложена направленность на выявление уровней владения способностями и перспектива развития способностей с помощью подобных заданий.
Результаты проверки обрабатываются статистически, что помогает в дальнейшем определять пути совершенствования приемов развития математических способностей младших школьников, разработки заданий новых типов и, в рамках методической вертикали, совместно с Институтом развития образования проводить соответствующие вебинары для учителей города, которые тоже становятся для нас традиционными.
Пример задания олимпиады, направленного на выявление и развитие математических способностей.
Дано уравнение (некоторые числа заменены фигурами, неизвестное число обозначено буквой х):
(х ∙▲∙ 4) : ■ = 32. Корень этого уравнения равен 4. Найдите корень уравнения (х ∙▲∙ 8) : ■ = 32 .
Здесь от участника требуется проявить гибкость мышления (умение направить мысль на «обратный» ход). Если ученик приводит несколько способов решения, то можно утверждать, что проявляется еще и вариативность мышления.
математическое умение – решение уравнения на основе взаимосвязи между компонентами и результатом действий – другого способа младшие школьники не знают.
Выполнение этого задания предполагает владение умением оперировать большим объемом информации и находить разные способы решения.
Большой потенциал для развития способностей имеют интеллектуальные и коммуникативные игры. Например, интеллектуальная игра «Умка» для первоклассников. Игра командная. Команду сопровождает учитель, из класса которого набрана команда. В процессе игры, сопровождающие находятся в аудитории вместе с командой и имеют возможность видеть, какие задания ученикам предлагаются и как их выполняют игроки. Все задания игры направлены на то, чтобы игроки проявили интеллектуальные способности в незнакомой для них ситуации. Задания носят надпредметный характер.
Выявление и развитие способностей младших школьников осуществляется на кафедре по нескольким направлениям.
Все представленные мероприятия направлены на достижение этой цели – выявление и развитие способностей младших школьников. Поэтому мы можем утверждать, что на кафедре начального образования сложилась определенная система, направленная на выявление и развитие способностей младших школьников нашего региона.
Список литературы:
- Голенкова А.С., Василенко А.С., Лысогорова Л.В Развитие математических способностей младших школьников посредством олимпиадных задач // Артемовские чтения. «Продуктивное обучение: опыт и перспективы». материалы XI Международной научной конференции. 2019. С. 123-127.
- Зубова С.П., Лысогорова Л.В. Математические олимпиады в современных условиях // Самарский научный вестник. 2013. № 3 (4). С. 61-63
http://izvestia-ippo.ru/zubova-s-p-lysogorova-l-v-vyyavlenie-i-r/