Заблоцкая Лариса Владимировна, ЧУ СОШ «Данко», магистрант института педагогики и психологии образования Московского городского педагогического университета, г. Москва. Е-mail: lariska199@yandex.ru
Заблоцкая Лариса Владимировна, ЧУ СОШ «Данко», магистрант института педагогики и психологии образования Московского городского педагогического университета, г. Москва. Е-mail: lariska199@yandex.ru
Научный руководитель: Козырева Нелли Арнольдовна, кандидат психологических наук, доцент департамента педагогики Института педагогики и психологии образования Московского городского педагогического университета, г. Москва. E-mail: kozyrevana@mgpu.ru
Статья посвящена разработке математической игры для старшего школьного звена. Был проведен анализ педагогических разработок, содержащих учебные игры по математике. На основе сделанных выводов была разработана математическая карточная игра для 9–11-х классов по тригонометрии.
Использование игр в образовательном процессе на сегодняшний день является перспективным направлением для развития педагогической и методической мысли. Многие педагоги адаптируют под игровое содержание учебный материал средней и старшей школы. Среди педагогических разработок можно найти много авторских игр по различным предметам среднего цикла, в том числе и по математике. Актуальность разработки игровых элементов на уроке для среднего и старшего школьного звеньев обуславливается положительным влиянием геймификации на мотивацию обучающихся [4].
Так, например, в статьях М. Е. Чумаковой [5] и А. Г. Королевой [2] можно найти сюжеты игр, в которые предметные задачи вошли непосредственно как одно из заданий игры. Данные примеры отображают суть применения игры как игровой оболочки с целью повышения мотивации к изучению и закреплению математического материала.
В рамках изучения математики возможно использование и настольных игр. Например, А. Ю. Леменевой описана карточная игра, в которой игровые задания представляют собой различного рода задачи по математике, алгебре и геометрии [3]. От того, насколько успешно решена игроком каждая задача, зависит движение карт в игре. Соответственно для того, чтобы скинуть все карты, игрок должен иметь достаточный уровень математических знаний. Стремление к победе мотивирует обучающегося к изучению математики. Как правило, разработанные настольные игры по математике направлены на закрепление уже полученного знания.
Нами разработана игра, в которой математическое знание было «вплетено» непосредственно в игровые правила. Так, разобравшись с правилами, игрок одновременно и получает возможность принять участие в партии, и изучает какой-либо математический факт. В ходе участия в партии игроку предоставлена возможность освоить и довести до автоматизма определение расположения точек на тригонометрической окружности, а также закрепить понятия синуса и косинуса числа. Данный математический материал изучается в старшей школе (9–11-е классы, в зависимости от учебной программы образовательного учреждения) и играет первостепенную роль в изучении такого раздела математики, как тригонометрия. В ходе анализа источников не было обнаружено разработок настольных игр по тригонометрии (в целом, по данному разделу игры существуют, но по большей части представляют собой квизы). Игра разработана на основе игры Uno и имеет схожую игровую механику, но некоторые правила игры видоизменены и адаптированы под конкретный учебный материал.
Название игры: трUгоNOметрия.
Возраст: 10–11-е классы общеобразовательной школы.
Цель игры: способствовать закреплению и автоматизации навыка определения точек на тригонометрической окружности.
Состав игры: колода карт, лист с игровыми правилами, заготовка единичной окружности в качестве игрового поля-подсказки (для новичков).
Колода состоит из 108 карт:
- 76 обычных карт;
- 8 специальных карт «пропуск хода»;
- 8 специальных карт «реверс»;
- 8 специальных карт «возьми 2»;
- 4 специальные карты «поменяй четверть»;
- 4 специальные карты «поменяй четверть и возьми 4».
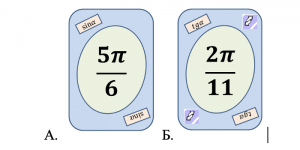
В центре каждой карты изображено значение угла, в верхнем левом и нижнем правом угла указана тригонометрическая функция (см. рисунок 1). Специальные карты отличаются от классических наличием значка в правом верхнем и левом нижнем углах. Например, на рисунке 1Б показана карта реверс. Цветовое оформление всех карт одинаковое и значения в игре не имеет.
Листок правил содержит описание необходимого математического знания. В данной игре, в отличие от классического Uno, вместо цвета и числа используются понятия «четверть» и «значение тригонометрической функции». Поэтому в правилах важно отразить, как работать с тригонометрической окружностью, и игрок должен ознакомиться с этой инструкцией прежде, чем начинать игру.
Рисунок 1. А) Макет обычной карты. Б) Макет специальной карты.
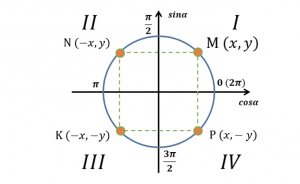
В правилах кратко рассказывается о том, как располагаются числа на тригонометрической окружности, акцентируется внимание на узловых точках (они же указаны на вспомогательном поле-окружности) и равенстве координат точек различных четвертей. Полезно оформить описание правил не сухим текстом, а с использованием большого количества иллюстративного материала и примеров. На наш взгляд важно также включение общей схемы определения равных значений синуса и косинуса на окружности (см. рисунок 2).
Ход игры. Игра рассчитана на 2-7 игроков. Каждому игроку выдается по 7 карт из общей колоды. Карты не показываются другим игрокам. Оставшиеся карты кладутся в отдельную колоду рубашкой вверх недалеко от центра поля-окружности. Верхняя карта снимается и кладется в центр игрового поля.
Далее игроки ходят по очереди «в положительном направлении тригонометрической окружности» (т. е. против часовой стрелки). Каждый игрок за один ход может сбросить одну карту, положив ее на верхнюю карту из центральной стопки.
Карту можно положить только в том случае, если:
- совпадают четверти, в которых находятся указанные на карточках значения;
- для чисел на картах совпадают значения тригонометрических функций, указанных в углах карт (например, по рисунку 2, на карту с числом Mс пометкой можно положить карту с числом Pс пометкой , несмотря на то, что сами числа лежат в разных четвертях).
Рисунок 2. Макет общей схемы правил и игрового поля
Если у игрока нет карт, которые он может сбросить, то он забирает верхнюю карту с колоды, причем может отыграть ее сразу же, если она подходит.
Специальные карты сбрасываются при тех же условиях, что и обычные, но обладают бонусным действием:
- «пропуск хода» — следующий игрок пропускает ход;
- «реверс» — меняет направление хода игры;
- «возьми 2» — следующий игрок берет 2 карты из общей колоды и пропускает ход;
- «поменяй четверть» — игрок получает право сменить играющую четверть;
- «поменяй четверть и возьми 4» — игрок получает право сменить играющую четверть, а следующий игрок берет 4 карты.
Когда игрок скидывает предпоследнюю карту, он должен произнести любое тригонометрическое выражение, равное единице. Например «синус квадрат альфа плюс косинус квадрат альфа», «два плюс косинус пи» или «синус пи пополам». Список с примерами фраз указан в листке правил, но игроки могут использовать и свои собственные примеры. Фразы не должны повторяться одним и тем же игроком в течение партии. По договоренности между игроками допустим вариант, при котором фразы не повторяются в течение партии даже разными игроками.
Если фраза не была произнесена или была допущена ошибка, то другие участники могут «подловить» игрока до того момента, как на поле будет положена следующая карта, и тогда тот берет две карты из общей колоды.
Победившим считается игрок, который скинул первым все карты. Оставшиеся места распределяются по количеству оставшихся карт. По договоренности между игроками, игра может продолжаться до тех пор, пока не останется только один игрок с картами на руках.
Нами разработан опытный образец игровой колоды. Проведена апробация игры на учениках 9-11-х классов, знакомых с базовыми понятиями тригонометрии. В ходе анализа полученных результатов было выявлено положительное влияние игры на скорость работы с тригонометрической окружностью: обучающиеся стали выполнять задания на определение соответственных точек окружности в различных координатных четвертях быстрее.
Игра будет полезна для применения в качестве разминки на уроках математики в старшей школе, а также во внеурочное время. Игра способствует автоматизации умения работать с окружностью мысленно: уметь представлять ее компоненты, находить приблизительное расположение точек на ней и устанавливать закономерности между синусами и косинусами различных углов.
Игра обретает новые правила прохождения для обучающихся по мере изучения учебного материала. Так, например, определение равных значений синусов и косинусов двух чисел возможно не только способом, описанным в правилах, но и с помощью формул приведения, которые по школьной программе изучаются после освоения основных навыков работы с окружностью. Таким образом, процесс игры в перспективе позволяет установить новые тригонометрические закономерности между числами даже в том случае, если материал еще не пройден.
Планируется разработка полноценной карточной математической игры с несколькими режимами и разными уровнями сложности на основе методики обучения тригонометрии. Например, можно ввести дополнительные режимы или специальные карты на доказательство тригонометрических тождеств, которые позволят игрокам отбиваться от карты «возьми 4».
Список литературы
- Волков Б.С. Возрастная психология. В 2-х ч. Ч. 1: От рождения до поступления в школу / Б.С. Волков, Н.В. Волкова. М.: Гуманитар. изд. центр ВЛАДОС, 2005. 366 с.
- Королева А.Г. Заключительный урок полугодия по математике: эффективность использования игровых технологий // European Association of pedagogues and psychologists «Science». 2014. С. 121–136.
- Леменева А.Ю. Значение настольных обучающих игр для уроков математики // Современный учитель дисциплин естественнонаучного цикла. Сборник материалов Международной научно-практической конференции. 2019. С. 229–231.
- Цаплина О.В. Игровые технологии в образовательном процессе // Ребенок в современном образовательном пространстве мегаполиса. Материалы VII международной научно-практической конференции, посвященной 25-летию МГПУ. 2020. С. 80–85.
- Чумакова Е.М. Игровые технологии на уроках математики // Университеты в системе поиска и поддержки математически одаренных детей и молодежи: материалы II Всероссийской научно-практической конференции. 2018. С. 99–102.
http://izvestia-ippo.ru/zablockaya-l-v-razrabotka-matematiches/