Вендина А.А., Киричек К.А. | Развитие математической одаренности младших школьников средствами схематизации

Вендина А.А., кандидат физико-математических наук, доцент   ФГАОУ ДПО «Академия Минпросвещения России», г. Москва

e-mail: aavendina@gmail.com

Киричек К.А., кандидат педагогических наук, доцент,  ГБОУ ВО СГПИ, г. Ставрополь

e-mail: KirichekKA@mail.ru

 Целью статьи является описание развития математических способностей (лежащих в основе математической одаренности) младших школьников средствами схематизации. Основу математической одаренности составляют три основных блока способностей (В. А. Крутецкий): 1) формализированное восприятие математического материала; 2) переработка математической информации; 3) хранение и запоминание математической информации. Для изучения вопроса развития математической одаренности средствами схематизации нами конкретизированы способности по переработке математической информации в контексте работы со схемами: 1) распознавание сходства и различий в графических структурах; 2) классификация, обобщение графических структур; 3) выявление закономерности; 4) быстрое и свободно переключение с графической модели на математическую или высказывательную и обратно; 5) преобразование графической структуры; 6) создание утверждений по заданной структуре. Проведенный анализ учебно-методических комплексов по математике показал, что обучение приемам схематизации в начальной школе происходит по двум направлениям: 1) работа с вычислительными схемами, 2) работа со схемами к текстовым задачам. На наш взгляд, для развития математических способностей средствами схематизации необходимо усилить выявленные два направления заданиями, направленными на развитие способностей по переработке математической информации в контексте работы со схемами.

Введение. В связи с тем, что понятие «математическая одаренность» — довольно сложное, комплексное и многоаспектное, на сегодняшний день существует несколько подходов к его определению. В этой работе мы остановимся на определении В. А. Крутецкого, который считал, что математическая одаренность – это совокупность математических способностей, обеспечивающих успешность личности в математической деятельности [4]. Данный подход позволяет выявить способности ребенка, составляющие основу математической одаренности. В. А. Крутецкий выделял три таких основных блока способностей:

1) формализированное восприятие математического материала, «схватывание» формальной структуры задания;

2) переработка математической информации;

3) хранение и запоминание математической информации.

Цель исследования. Способности обучающихся не являются неизменными, они развиваются в процессе учения, предполагающего постоянное включение школьника в познавательную и исследовательскую деятельность. Так, Л. П. Стойлова отмечает, что «в процессе изучения математики способности школьников развиваются, но стихийно и не у всех учащихся» [5]. Поэтому для формирования и развития математических способностей младших школьников необходима специальная, систематическая, правильно организованная деятельность с использованием возможностей программного материала начального курса математики. В связи с чем целью статьи является описание развития математических способностей (лежащих в основе математической одаренности) младших школьников средствами схематизации.

Методика. Изучение математики на начальном этапе предполагает освоение обучающимися графических способов представления информации, решения заданий и развитие навыков по работе с графической информацией.

Отметим, что печатные учебники и учебные пособия по математике начальной школы содержат большое количество различных схем и графических моделей. Как правило, они выступают средством демонстрации решения или условия. В то же время опыт использования интерактивных моделей обучающей платформы Яндекс.Учебник обнаруживает значительные трудности младших школьников в применении схем в практической деятельности. Чаще всего, обучающиеся затрудняются в «чтении» схем, а также в составлении моделей в виде схем к различным заданиям.

Анализ учебно-методических комплексов по математике («Школа России», «Школа 21-го века», «Перспектива») позволил нам установить, что обучение приемам схематизации в начальной школе происходит по следующим направлениям.

• Работа с вычислительными схемами. Здесь следует выделить:
• схемы, с помощью которых осуществляется нахождение неизвестных компонентов арифметических действий;
• схемы, демонстрирующие свойства арифметических действий;
• схемы для изучения вычислительного приема;
• числовые ребусы.

Приведем примеры заданий на работу с вычислительными схемами.

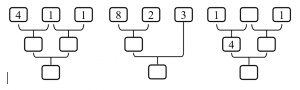
Задание 1. Числа, соединенные линией, нужно сложить. Заполни схемы (рисунок 1) по этому правилу.

Рисунок 1 – Вычислительная схема сложения и вычитания

Задание 2. Составь равенство к схеме (рисунок 2).

Рисунок 2 – Схема распределительного свойства

• Работа со схемами к текстовым задачам. Здесь следует отметить, что схемы к текстовым задачам определяются типом задачи. В начальной школе чаще всего рассматривают типовые схемы к следующим видам задач:
• на целое и части;
• на разностное и кратное сравнение;
• на различные процессы (движение, работу, «куплю – продажу» и т.п.) с пропорциональными величинами.

Также рассматриваются схемы к стохастическим (комбинаторным) задачам, логическим и нестандартным задачам.

Обучение решению текстовых задач предполагает воспроизведение структуры математической задачи из ее контекста и работу с ней. Структура задачи позволяет визуализировать и интерпретировать отношения между объектами, в связи с чем она может быть представлена с помощью графических объектов и математических символов.

В работе [3] отмечается, что переход от текста задачи к ее структурной модели требует осмысленного чтения от обучающихся; умения выделять составные части задачи, устанавливать взаимосвязи между величинами, заданными в явном и неявном виде. Это подразумевает, что развитие математических способностей обучаемых напрямую связано с развитием навыков смыслового и функционального чтения, а работа с математическими задачами служит средством их формирования [2].

Результаты. В соответствии с указанными информационными блоками математических способностей нами конкретизированы способности по переработке математической информации в контексте работы со схемами:

• распознавание сходства и различий в графических структурах;
• классификация, обобщение графических структур;
• выявление закономерности;
• быстрое и свободно переключение с графической модели на математическую или высказывательную и обратно;
• преобразование графической структуры;
• создание утверждений по заданной структуре.

Работа со схемами может быть организована с возможностью интерактивного взаимодействия с ними. В частности, на образовательной платформе «Яндекс.Учебник», в разделе «Текстовые задачи» представлен соответствующий комплекс заданий по работе со схемами. Приведем пример одного из таких заданий.

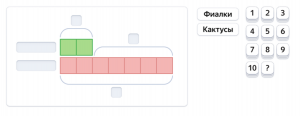
Задание 3. Прочитай задачу и дополни схему к ней (рисунок 3). Обозначь неизвестное на схеме знаком вопроса. Задача: «У Светланы на подоконнике стоят в горшочках 2 кактуса, а фиалок – на 5 больше. Сколько фиалок у Светланы?»

Рисунок 3 – Интерактивная схема к задаче

Сведения о выполнении заданий на платформе «Яндекс.Учебник» показывают, что с первой попытки справляются с данным заданием 34% младших школьников, что свидетельствует о том, что обучающиеся испытывают затруднения в распознавании структуры текстовой задачи и в дополнении схемы недостающими данными.

Обсуждение. На наш взгляд, для развития математических способностей средствами схематизации необходимо усилить выявленные два направления обучения приемам схематизации в начальной школе (1 – работа с вычислительными схемами, 2 – работа со схемами к текстовым задачам) заданиями, направленными на развитие способностей по переработке математической информации в контексте работы со схемами.

Приведем примеры заданий, способствующих формированию некоторых указанных нами способностей.

Задание 4. Соедини задачу с верной схемой.

Это задание позволяет выявить одну и ту же математическую структуру у внешне различных задач: на прямую и косвенную формы. Такого типа задания формируют способность к обобщению моделей текстовых задач.

Корректное построение схемы к условию задачи помогает в анализе ситуации, описанной в ней, и может определить способ ее решения. Рассмотрим пример такого задания.

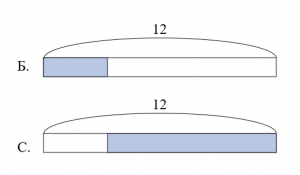
Задание 5 [1]. У брата и сестры было по 12 грецких орехов. Брат съел несколько орехов, а сестра съела столько орехов, сколько их осталось у брата. Сколько орехов осталось у них вместе?

Рисунок 4 – Схема к задаче 5

Закрашенные части прямоугольников на рисунке 4 соответствуют числу съеденных орехов, значит, не закрашенные – числу несъеденных. Методом наложения нетрудно увидеть, что как съеденных, так и несъеденных орехов – по 12. Здесь имеет смысл формировать способность переключаться с графической модели на математическую или высказывательную и обратно.

Заключение. Одним из направлений работы по развитию математической одаренности является формирование способностей работы с графическими образами, графическими моделями – схемами. Схемы при этом могут выступать средством получения нового знания и (или) в качестве визуального образа, иллюстрирующего структурные связи внутри объекта или между объектами. Нами предложено развивать математическую одаренность младших школьников средствами схематизации, наряду с прочими средствами, т.к. схематические структуры представляют собой средство познания, развития мышления и математических способностей. Перспективы исследования заключаются в изучении возможностей включения работы со схемами с целью развития математической одаренности на уровне основного общего образования.

 

Список литературы

1. Захарова О.А. Математика в вопросах и заданиях. 4 кл.: тетрадь для самостоятельной работы № 1 / О.А. Захарова, Е.П. Юдина: под. ред. Р.Г. Чураковой. – 8-е изд., стреотипное, М.: Академкнига/Учебник, 2021. – 96 с.
2. Кокорева В.В., Вендина А.А., Андрухив Л.В. Стратегии смыслового чтения в процессе обучения решению текстовых задач в начальной школе // Kant. – 2021. – № 4 (41). – С. 261-265.
3. Кокорева В.В., Вендина А.А., Богомолов Е.В. К вопросу обучения младших школьников моделированию при решении текстовых задач // Вопросы педагогики. – 2019. – № 6-1. – С. 46-51.
4. Крутецкий В.А. Психология математических способностей школьников / Под ред. Н.И. Чуприковой. – М.: Издательство «Институт практической психологии»; Воронеж: Издательство НПО «МОДЭК», 1998. – 416 с.
5. Стойлова Л.П. Развитие математических способностей у младших школьников в современных условиях // Начальная школа. – 2013. – № 11. – С. 56-57.

Abstract. The purpose of the article is to describe the development of mathematical abilities (underlying mathematical giftedness) of younger schoolchildren by means of schematization. The basis of mathematical giftedness consists of three main blocks of abilities (V. A. Krutetsky): 1) formalized perception of mathematical material; 2) processing of mathematical information; 3) storage and memorization of mathematical information. To study the issue of the development of mathematical giftedness by means of schematization, we have concretized the ability to process mathematical information in the context of working with schemes: 1) recognition of similarities and differences in graphic structures; 2) classification, generalization of graphic structures; 3) identification of patterns; 4) fast and free switching from a graphical model to a mathematical or utterance model and vice versa; 5) transformation of a graphic structure; 6) creation of statements according to a given structure. The analysis of educational and methodological complexes in mathematics has shown that teaching schematization techniques in primary school occurs in two directions: 1) work with computational schemes, 2) work with schemes for text tasks. In our opinion, for the development of mathematical abilities by means of schematization, it is necessary to strengthen the identified two directions with tasks aimed at developing the ability to process mathematical information in the context of working with schemes.

Keywords: mathematical giftedness; scheme; text problem; elementary school.