Романова М.А., Вендина А.А. | РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ ПОСТРОЕНИЯ ГРАФОВ

УДК 372.47

Романова М.А., доктор психологических наук, доцент, профессор департамента методики обучения Института педагогики и психологии образования Московского городского педагогического университета, г. Москва. E-mail:romanovam@mgpu.ru

 Вендина А.А., канд. физ.-мат. наук, доцент, методист образовательного проекта Яндекс.Учебник, г. Москва. E-mail: aavendina@gmail.com

 Материалы VIII Всероссийской научно-практической конференции «РЕБЕНОК В СОВРЕМЕННОМ ОБРАЗОВАТЕЛЬНОМ ПРОСТРАНСТВЕ МЕГАПОЛИСА»

Работа носит практико-ориентированный характер. В ней рассматриваются особенности логических задач, сформулировано основное отличие логической задачи от текстовой сюжетной, являющихся предметом рассмотрения в школьном курсе математики. В работе приводятся примеры логических заданий, которые могут быть решены с помощью построения графа или дерева возможных вариантов. Построение графа приводится применительно к задаче на установление соответствия между двумя множествами объектов. Работа будет полезна учителям математики, а также студентам высшего педагогического образования

Развитие логического мышления – одна из задач школьного образования. Математика, как учебный предмет, обладает различными средствами выполнения этой задачи, а особая роль в формировании указанного типа мышления принадлежит логическим задачам, рассматриваемым как на начальном этапе обучения математике, так и в курсе математики основной и старшей школах.

Заметим, что сам термин «логическая задача» носит весьма условный характер, поскольку назвать логическими можно многие задачи дивергентного типа. Эта терминология используется в стандартах второго поколения и считается понятной, поскольку существует достаточно литературы, содержащей задачи с таким названием, но в настоящее время понятие «логическая задача» не имеет однозначного определения. В работе [4, с. 5] описываются следующие особенности логических задач:

• решение логических задач больше напоминает процесс исследования;
• очень часто отсутствуют какие-либо арифметические действия;
• ответ на вопрос задачи получается согласно правилам логического вывода.

Свидетельством развитости логического мышления младших школьников является продуктивность мышления при решении логических задач и задач дивергентного типа.

В отличии от сюжетных текстовых задач, на наш взгляд, в ходе построения плана решения логических задач ключевым является не нахождение количественных характеристик объекта, а определение и анализ отношений между всеми объектами задачи. Поэтому, именно логическая задача создает возможности для достижения оригинального результата посредством анализа, сопоставления и сочетания большого количества вариантов. При этом решение логических заданий, как правило, требует от учеников умений проводить рассуждения, устанавливать причинно-следственные связи, выдвигать и доказывать гипотезы, находить рациональные способы решения задания [2]. Поскольку в задаче на логику даются отношения между предметами и следуя по цепочке этих отношений, необходимо прийти к ответу на вопрос, то задачи данного типа чаще всего решаются с помощью построения вспомогательных графических моделей, схем и таблиц. А среди различных вариантов графического моделирования выделяют графы и их частный случай – дерево возможных вариантов [3].

Процесс рассуждения при решении задач с «выращиванием дерева» гармонично объединяет теорию множеств, элементы математической логики, теории вероятностей, математической статистики и комбинаторики, вооружает учащихся навыками моделирования, комбинирования, анализа, а также влияет на формирование таких качеств мышления, как гибкость, избирательность и т.п.

Графические модели способствуют освоению младшими школьниками рациональных приемов решения нестандартных заданий на основе схематизации и моделирования. Использование дерева рассуждений в процессе решения логических задач способствует повышению наглядности и упрощает рассуждения ученика. С помощью графа ученики представляет все возможные ситуации, обсуждаемые в задаче. При этом, как отмечается в работе А.С. Серба и К.А. Киричек [5] «не каждая задача может быть решена с использованием графового моделирования. Необходимо подбирать наиболее рациональный способ решения, исходя из условия задачи, а не ставить самоцелью».

Напомним, что графами называют геометрические фигуры, состоящие из точек (вершин) и линий их соединяющих (ребер). При этом с помощью вершин изображают элементы некоторого множества предметов, людей, числовых и письменных ходов, с помощью ребер – определенные связи между элементами.  При некоторых дополнительных условиях граф называется «деревом». В том случае, если играет роль направление действия или правильная последовательность в изображении объектов, связь между элементами каждого графа необходимо обозначать стрелками. В случае применения графа как основы поиска плана решения логических задач, вершины и ребра графа следует рассматривать контексте связей, отраженных в задаче, и придавать определенный смысл.

В школьном курсе математики графовое моделирование рассматривается применительно к задачам вида [1]:

• комбинаторные и вероятностные задачи. Среди комбинаторных задач выделяют задания на размещения из n элементов по 2.
• задачи, в которых устанавливаются соответствия между элементами двух множеств.

Далее рассмотрим пример логического задания, в которых рассматриваются объекты двух множеств. Сформулируем правило составления графа для указанного типа задач:

• Если объект одного множества связан заданным свойством с объектом другого множества, то, изображающие эти объекты точки, можно соединить сплошной линией.
• Если какая-то из точек окажется соединенной с двумя точками другого множества пунктирными линиями, то с третьей точкой она должна быть соединена не пунктирной, а сплошной линией.

Задача [1, с. 98]. Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?

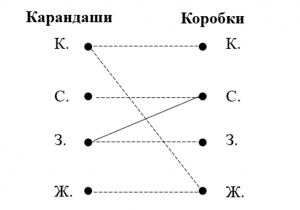
Решение. Карандаши и коробки обозначим точками на рисунке. Цвет укажем соответствующими заглавными буквами. Проведем на рисунке линии пунктирные и сплошные линии, которые будут обозначать отсутствует или находится в коробке карандаш соответственно. Изобразим это на вспомогательном рисунке. Получаем следующий граф (рис. 1).

Рисунок 1. Вспомогательный граф к заданию 1

Получить заполненный граф или «вырастить дерево» для решения данной задачи помогут рассуждения, выстроенные в ниже приведенном логическом порядке.

• По условию задачи, в каждой коробке только один карандаш, а карандаш зеленого цвета находится в синей коробке, согласно условию задачи, то можно соединить пунктирными линиями точки К. и Ж. столбца «Карандаши» с точкой С. столбца «Коробки».

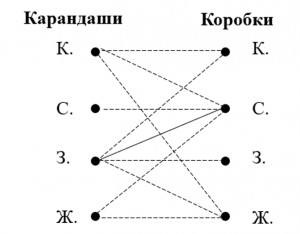
Рассуждаем аналогичным образом и проводим пунктирные линии от точки З. левого столбца к точкам К., С. и Ж. правого столбца, так как зеленый карандаш уже нигде лежат не будем. Получим промежуточный граф (рис. 2).

Рисунок 2. Промежуточный граф к заданию 1

• После выполнения первого шага решения от точки К. в столбце «Карандаши» ведут три пунктирные линии к трем точкам в столбце «Коробки» — к точкам К., С., Ж. Значит, в зеленой коробке лежит красный карандаш, что необходимо отразить сплошной линией на графе.

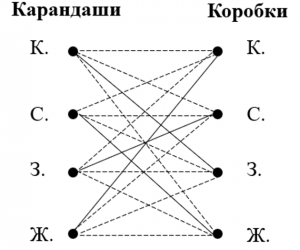
Далее рассуждаем аналогично, в результате чего получим заполненный граф, представленный на рис. 3.

Рисунок 3. Заполненный граф к заданию 1

Задача 2. Катя сложила в три непрозрачные коробочки по 2 елочных украшения – синие и красные шарики, но все надписи на коробках она перепутала. Помоги Кате узнать содержимое каждой коробочки, если можно достать только один шарик и только из одной коробки.

Рисунок 4. Вспомогательный граф к заданию 2

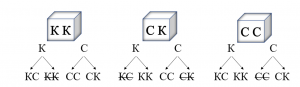
Решить подобную задачу можно с помощью построения дерева решений. Обратим внимание, что это частный случай дерева. Характерной отличительной особенностью такого дерева является то, что «растет» оно не снизу вверх, а сверху вниз. Именно данный вид графа удобен для расположения объектов в нужной последовательности.

С этой целью необходимо составить возможные варианты размещения шаров в каждой коробке. Так как надписи перепутаны, мы зачеркнули невозможные исходы (рис. 2). При этом варианты «КС» и «СК» считаются одинаковыми, так как расположение шаров в коробке незначимо.

Рисунок 5. Дерево возможных решений

Мы видим, что Кате нужно достать шарик только из коробки с надписью «СК». Если шарик при этом будет красного цвета, значит в этой коробке лежат 2 красных шариках, тогда в коробке справа лежат красный и синий шарики, а в коробке слева – оба синих шарика. Аналогичным образом рассуждаем, если шарик из коробки, расположенной, посередине, Катя достанет синее украшение.

Видим, что рассмотрение «дерева» в качестве фундамента или опоры для построения хода рассуждений в процессе поиска плана решения задачи и использование графов в качестве объектов наглядности способствует эффективному переводу текста на язык моделирования и удерживать в поле зрения и запоминать гораздо больше фактов и связей, содержащихся в тексте задачи, устанавливать между ними зависимости.

Поэтому пропедевтику идей и методов теории графов надо начинать с начальной школы. Первое знакомство с элементами этой теории не требует специальной математической подготовки. А так как задачи, решаемые с помощью графов, разнообразны, нестандартны, и, как правило носят занимательный характер, то они воспринимаются детьми с большим интересом и вниманием.

Наш опыт показывает, что предлагаемые способы решения задач не только позитивно воспринимаются и усваиваются младшими школьниками с высокой степенью успешности, но и дают им возможность использовать элементарные методы моделирования и комбинаторного анализа для поиска и построения плана решения задач дивергентного типа. Младший школьный возраст, на наш взгляд, является наиболее сензитивным периодом для знакомства с графами и наглядной комбинаторикой, а умение «выращивания дерева» – предиктором успешности решения любой логической задачи.

 

Список литературы

1. Богомолов Е.В. Элементы стохастики в начальной школе / Е.В. Богомолов, А.А. Вендина // Вопросы педагогики. 2019. № 1. С. 8-11.
2. Калиниченко А.В., Романова М.А. Элементы логики в начальной школе / А.В. Калиниченко, М.А. Романова // Начальная школа. 2020. № 9. С. 66-67.
3. Кокорева В.В. Графические модели как средство визуализации текстовых задач в начальной школе / В.В. Кокорева, А.А. Вендина // Kant. 2020. № 3 (36). С. 284-289.
4. Кондрашова З.М. Логические задачи в начальной школе: технологии обучения / З.М. Кондрашова, Н.Н. Солохин. – Изд.- 2-е. – Ростов н/Д: Феникс, 2017. – 137 с.
5. Серба А.С. Формирование у обучающихся умения решать задачи практического характера на основе использования теории графов / А.С. Серба, К.А. Киричек // Вестник Белгородского института развития образования. 2019. Т. 6. № 2 (12). С. 101-107.