Матвеева В.А., Воронюк Ю.Д. | МОДЕЛИРОВАНИЕ КАК СМЫСЛООБРАЗУЮЩИЙ ФЕНОМЕН ПРИ РЕШЕНИИ ЗАДАЧ ПО МАТЕМАТИКЕ

Матвеева В.А., Федеральное государственное бюджетное образовательное учреждение высшего образования «Сахалинский государственный университет», старший преподаватель кафедры математики Института естественных наук и техносферной безопасности,  г. Южно-Сахалинск, e—mail: matveeva89.ru@mail.ru

Воронюк Ю.Д., Федеральное государственное бюджетное образовательное учреждение высшего образования «Сахалинский государственный университет», студент направления подготовки «Педагогическое образование (с двумя профилями подготовки)», профиль «Математика и физика», г. Южно-Сахалинск, e—mail: y_lisovskaya19@mail.ru

 Материалы VIII Всероссийской научно-практической конференции «РЕБЕНОК В СОВРЕМЕННОМ ОБРАЗОВАТЕЛЬНОМ ПРОСТРАНСТВЕ МЕГАПОЛИСА»

В статье рассматривается моделирование, в частности математическое моделирование, как необходимый инструмент для построения современной образовательной среды, как смыслообразующий феномен, позволяющий достигать метапредметных результатов в образовании, в частности при освоении предметной области «Математика». Рассмотрены различные типологии задач в школьном курсе математики. Задачей данной работы является анализ системы школьных задач в предметной области «Математика» и актуализация типологии задач, что обусловлено ускорением процессов информационного взаимодействия в современном обществе, требованиями системно-деятельностного подхода в образовании. Результатом работы является актуализация системы школьных задач в соответствии с типологией, основанной на способах обработки, представления информации.

 

Глобальная коммуникация современного общества становится мощным инструментом, влияющим на объективную реальность. Все аспекты социального взаимодействия благодаря компьютерным технологиям превращаются в динамическое единое информационное взаимодействие. Информационная культура становится основой общей культуры современного человека, поэтому умение обрабатывать, создавать, систематизировать информацию является важным элементом взаимодействия в мировом информационном пространстве.

Технические и технологические процессы, обеспечивающие динамичность и масштабность информационных процессов, влияют также на образовательную среду. На сегодняшний день задача учителя заключается не в «передаче знаний», а в формировании умения учиться, добывать, обрабатывать, создавать информацию. «Умение учиться» является сегодня центральной идеей в построении образовательной траектории. В Федеральных государственных образовательных стандартах (ФГОС) для начального общего образования (ФГОС НОО), а также для основного общего образования (ФГОС ООО) особое внимание уделяется требованиям к достижению метапредметных результатов «включающих освоенные обучающимися межпредметные понятия и универсальные учебные действия» [1, стр. 5].

Достижение метапредметного результата в образовании предполагает умение работать с информацией «создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач» [1, стр. 7], а также «устанавливать аналогии, классифицировать,  устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы» [1, стр. 7]. Таким образом, информация, информационные процессы играют ключевую роль в современном информационном обществе, в котором научные, технические, социальные аспекты рассматриваются в концепции единого информационного  взаимодействия.

Во многих педагогических исследованиях (С. А. Бешенкова, Е. А. Ракитиной, М. И. Шутиковой и др.) подчёркивается обширность междисциплинарных связей информатики с другими науками, прежде всего с математикой, так как построение компьютерных моделей основано на математическом моделировании. В современном образовании понятию «модель» отводится ключевое значение. Так как модель является результатом семиотической, знаково-символической деятельности при анализе данных, необходимых для принятия решения, описания предмета познания, явления окружающей действительности. Информационные процессы затрагивают различные сферы деятельности человека, различные по своей природе, но единые по природе информационных процессов, о которой говорил ещё во второй половине XX века академик А. П. Ершов. Именно поэтому сегодня в рамках «метапредметных» связей рассматриваются предметные области «Математика» и «Информатика», так как они способны описывать другие системы различной природы. Таким образом, моделирование приобретает некую смыслообразующую функцию в современном образовании, является интегративной основой в процессе информационного взаимодействия [2].

Знаковая система, формализация, математическое моделирование (частный случай информационного моделирования) являются неотъемлемой частью математики. Обратим свое внимание на текстовые задачи, они уже являются некоторой информационной либо математической моделью. Как правило, работа с текстовой задачей сопровождается некоторой дополнительной формализацией представленной словесной модели. В литературе можно встретить классификации текстовых задач по различным основаниям: 1) по количеству действий (простые, составные); 2) по соотношению условий и требований (неопределенные, определенные, с альтернативным условием); 3) по характеру требований (нахождение искомых, доказательство или объяснение, преобразование или построение); 4) по фабуле задачи (на работу, движение, проценты, доли и дроби, куплю-продажу и др.) 5) по методу решения (арифметические, алгебраические, геометрические, комбинированные) и др. Заметим, что любая классификация текстовых задач является условной и зависит от ряда факторов: цель обучения, степень проблемности и др.

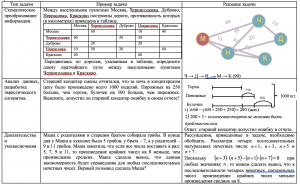
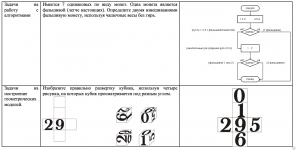
В контексте современного информационного подхода в образовании считаем необходимым актуализировать типологию текстовых задач по способу обработки, представления информации. Выделим следующие типы задач: 1) схематическое преобразование информации; 2) анализ данных, разработка эвристического алгоритма; 3) доказательства и умозаключения; 4) алгоритмы; 5) построение геометрических моделей [3].

К первому типу можно отнести задачи, предметом проверки которых является умение использовать разнообразные формы представления информации: графы, таблицы, графики, рисунки, диаграммы, условные рисунки, и др. При этом составление или интерпретация математической модели является для данного типа задач основой. Ко второму типу задач отнесем задачи, для решения которых необходимо провести анализ данных и произвести некий поиск решения, возможно произвести решение несколькими способами (разработать эвристический алгоритм). Задачи, относящиеся к данному типу, могут быть как стандартные сюжетные, так и нестандартные, требующие творческого подхода. Задачи третьего типа (на доказательства и умозаключения) играют важную роль. Доказывать, устанавливать причинно-следственные связи, правильно использовать умозаключения, все это нужно не только для математиков, как сказал Владимир Игоревич Арнольд: «Тот, кто не научился искусству доказательства в школе, не способен отличить правильное рассуждение от неправильного» [4, с. 9]. С алгоритмами мы сталкиваемся далеко за пределами учебной деятельности действуя по определенным правилам, следуя инструкциям и предписаниям. Задачи на работу с алгоритмами позволяют формировать когнитивную составляющую предметной области в контексте информационного подхода. Задачи на построение геометрических моделей способствуют формированию образного, в частности пространственного мышления, что является необходимым условием взаимодействия технологий и человека. Образы представляют собой средство моделирования процессов и явлений.

Приведем несколько примеров математических задач согласно представленной типологии (таблица 1.).

 

С развитием общества связь между математикой и информатикой становится не просто очевидной, а необходимой, и это мы показываем на уроках математики. Представленная нами типология задач является естественным результатом актуализации системы задач в рамках учебного материала в предметной области «Математика». Данный подход помогает структурировать систему задач, отвечающую принципам современной образовательной парадигмы, основанной на информационном подходе. Таким образом, обучение моделированию на уроках математики нисколько не ущемляет процесс формирования когнитивной составляющей при освоении предметной области, а напротив, дополняет и оптимизирует данный процесс. В завершении хочется вспомнить слова Игоря Федоровича Шарыгина: «Целью математики является не получение знания, а сам процесс обучения» [5]. Математика и информатика представляют оптимальную образовательную среду со всеми инструментами необходимыми для достижения метапредметных результатов. Проведенное исследование нуждается в продолжении и апробации полученных теоретических выводов.

 

Список литературы

1. Федеральный государственный образовательный стандарт основного общего образования. Утвержден приказом Министерства образования и науки Российской Федерации от 17 декабря 2010 г. № 1897 [Электронный ресурс]//Федеральные государственные образовательные стандарты. – Режим доступа: https://fgos.ru/ (дата обращения: 09.03.2021).
2. Бешенков С.А., Шутикова М.И., Э.В. Миндзаева Конвергенция информатики и технологии в контексте вызовов цифрового социума / С.А. Бешенков, М.И. Шутикова, Э.В. Миндзаева // Конференциум АСОУ: сборник научных трудов и материалов научно-практических конференций. 2017. № 4. С. 39 — 46.
3. Матвеева В. А. Теоретико-методические основы развития ИКТ-компетентности у будущих учителей начальных классов / В.А. Матвеева // Известия института педагогики и психологии образования: электронный журнал. – М.: «Московский городской педагогический университет» институт педагогики и психологии образования. 2020. № 2/2020. С.143-148. URL: http://izvestia-ippo.ru. Регистрационный номер: № ФС77-68116
4. «Математическая безграмотность губительнее костров инквизиции» Памяти Владимира Игоревича Арнольда, публикация Плотовского Г. М. // Математика и высшем образовании. – 2010. – № 8. – С. 7-18. URL:  http://www.mvo.unn.ru/files (дата обращения: 09.03.2021).
5. Математическое образование в XXI веке («НГ-Наука», N 9 18 октября 2000 года, стр. 12-14) [Электронный ресурс]. Режим доступа: https://www.mccme.ru/conf2000/statia1x.html (дата обращения: 09.03.2021)

The article considers modeling, in particular mathematical modeling, as a necessary tool for building a modern educational environment, as a meaning-forming phenomenon that allows achieving metasubject results in education, in particular when mastering the subject area «Mathematics». Various typologies of problems in the school mathematics course are considered. The purpose of this work is to analyze the system of school tasks in the subject area «Mathematics» and update the typology of tasks, which is due to the acceleration of the processes of information interaction in modern society, the requirements of the system-activity approach in education. The result of the work is the updating of the system of school tasks in accordance with the typology based on the methods of processing and presenting information.

Keywords: modeling, typology of text problems.