Матвеева Валентина Александровна, кандидат педагогических наук, доцент кафедры математики Института естественных наук и техносферной безопасности
ФГБОУ ВО «Сахалинский государственный университет», г. Южно-Сахалинск.
e-mail: matveeva89.ru@mail.ru
Голубкова Дарья Александровна, студентка 2 курса направления подготовки «Педагогическое образование», профиль «Начальное образование», Институт психологии и педагогики
ФГБОУ ВО «Сахалинский государственный университет», г. Южно-Сахалинск.
e-mail: daria.golubkova03@mail.ru
Изменения, происходящие в настоящее время в социальной, экономической, культурной жизни современного цифрового общества оказывают существеное влияние на теорию и практику учебно-воспитательного процесса. Согласно ФГОС НОО исследовательская деятельность младшего школьника является составляющей внеучебной деятельности младшего школьника, также указано, что при освоении предметной области «Математика и информатика» одним из приобретенных умений является «исследовать». В статье рассмотрен подход по формированию исследовательских умений у младших школьников при решении текстовых задач по математике. Выстраивая систему задач в определенной последовательности, мы моделируем ситуацию поэтапного классического исследования. В основе данной методики лежит понимание исследовательских умений психологом А.И. Савенковым.
The changes currently taking place in the social, economic, cultural life of the modern digital society have a significant impact on the theory and practice of the educational process. According to the Federal State Educational Standard of the IEO, the research activity of a younger student is a component of the extracurricular activities of a younger student, it is also indicated that when mastering the subject area «Mathematics and Informatics», one of the acquired skills is «research». The article considers an approach to the formation of research skills in younger students in solving text problems in mathematics. By building a system of tasks in a certain sequence, we model the situation of a phased classical study. This technique is based on the understanding of research skills by psychologist A.I. Savenkov.
Согласно Федеральным государственным образовательным стандартам начального общего образования, исследовательская деятельность младшего школьника является составляющей внеучебной деятельности учеников начальных классов. Развитие исследовательских умений у школьников реализуется в основном через проектную деятельность, которая требует соблюдения определенных этапов. Хочется отметить, что основные этапы исследовательской работы могут быть отражены при решении текстовых задач при обучении математике. Данный подход требует соблюдения определенных условий: 1) вопросы задачи должны отражать суть определенного исследовательского умения; 2) решение задач происходит в установленном порядке; 3) типология задач отражает этапы исследовательской работы.
Вопросами формирования исследовательских умений младших школьников занимаются такие ученые как И.А. Ильницкая, П.Я. Гальперин, В.В. Давыдов, Н.А. Менчинская, Н.Ф. Талызина, Б.М. Теплов, Д.Б. Эльконин, А.И. Савенков и др.
Под исследовательскими умениями Александр Ильич Савенков понимает «умения видеть проблемы, задавать вопросы, выдвигать гипотезы, давать определения понятиям, классифицировать, наблюдать, проводить эксперименты, делать выводы и умозаключения, структурировать материал, работать с текстом, доказывать и защищать свои идеи» [3].
Таблица 1.
Типология задач, направленна на развитие исследовательских умений у младших школьников.
| Исследовательские умения (по А.И. Савенкову) | Типы задач |
| Видеть проблемы | Задачи на умение видеть проблемы |
| Вырабатывать гипотезы | Задачи на выработку гипотез |
| Наблюдать | Задачи на формирование умения наблюдать |
| Проводить эксперименты | Задачи на умение экспериментировать |
| Давать определение понятиям | Задачи на умение давать определения |
| Добывать информацию | Задачи на умение работать с информацией |
| Проводить самостоятельное исследование | Задачи на умение исследовать |
| Делать сравнения | Задачи на умение сравнивать объекты |
| Давать оценку | Задачи на умение оценивать |
| Доказывать правильность точки зрения | Задачи на умение доказывать правильность точки зрения |
| Составлять внутренний план умственных действий | Задачи на составление внутреннего плана действий |
| Формулировать суждения | Задачи, на умение формулировать суждения |
Согласно представленной типологии, рассмотрим примеры текстовых задач.
- Задачи на формирование умений видеть проблемы, задавать вопросы.
Задача: известно, что периметр одного прямоугольника больше периметра другого прямоугольника. Сравните площади этих прямоугольников.
Комментарий: в данной задаче нельзя дать однозначный ответ. Этот факт вызывает определенную проблему. Необходимо рассмотреть возможные варианты сторон этих прямоугольников и вычислить их периметр и площадь. Перебирая различные комбинации, учащийся должен увидеть, что существует 3 возможных варианта:
1) площадь прямоугольника с большим периметром может быть больше плошади другого прямоугольника;
2) площадь прямоугольника с большим периметром может быть меньше плошади другого;
3) площади могут быть равны.
Решение таких задач предполагает дискуссию учителя с учениками. Как правило, школьники заблуждаются в своих предположениях. Кажется совершенно очевидным, что у прямоугольника с большим периметром площадь также больше, но в ходе рассуждений оказывается, что решение не так однозначно. Ситуация может оказаться проблемной после ряда вопросов: действительно ли площади равны или площадь одного прямоугольника больше другого? А как это проверить?
- Задачи с ошибками. Задачи с проблемными ситуациями.
Задача: из пунктов А и В, расстояние между которыми 70 км, отправились одновременно пешеход и велосипедист со скоростями 5 км/ч и 15 км/ч соответственно. Какое расстояние будет между ними через 3 ч?
Комментарий:
1) Для начала следует разобраться, какой в этой задаче тип движения: встречное/в одном направлении/ в противоположных направлениях?
2) Далее нужно обратить внимание на участников процесса, определить, из какого пункта вышел пешеход и велосипедист.
3) Необходимо заметить, что данных не хватает, важно разобраться, является ли это опечаткой или задачу можно всё-таки решить?
4) Если решить можно, то каким образом?
5) Задача может иметь несколько решений?
Такая задача нестандартная в силу недостающих данных, но именно это создаёт проблемную ситуацию, заставляет школьников размышлять, искать решение, используя при этом исходное условие. Заметим, что в данной задаче должно быть рассмотрено 3-и ситуации, соответствующие 3-м типам движения. Соответственно, получаем неоднозначное решение.
- Задачи на выработку гипотез.
Задача: «Найди возможную причину события»
Установите причинно-следственную связь между событиями:
«На парте лежит прямоугольник, вырезанный из картона».
«На парте лежат равные треугольники».
Комментарий: в традиционном исследовании школьник формулирует гипотезу в своей исследовательской работе. Данный тип задач поможет сформировать такое умение. В данном случае устанавливается причинно-следственная связь между явлениями. Очевидно, что прямоугольник разрезали по диагонали в результате чего были получены равные треугольники.
- Задачи на умение давать определения.
А) «Назови одним словом»
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – это …
Треугольник, прямоугольник, квадрат – это …
Б) «Отгадай»
Педагог загадывает предмет, дает его словесное описание, дети пытаются отгадать его. Затем роль ведущего передается детям. Игра проводится три-четыре раза. По ходу игры педагог следит за тем, чтобы дети давали как можно больше характеристик предмету.
Комментарий: в первом задании можно задать дополнительный вопрос: что объединяет перечисленные символы и геометрические фигуры? Какие признаки на это указывают? Объясните свой ответ. Во втором случае учителю можно назвать как можно больше характеристик предмета и акцентировать внимание на каждой из них, чтобы по аналогии дети могли придумать описание своего загаданного предмета.
Например, загаданное слово – мяч, учитель говорит: «предмет может быть тяжелым и лёгким, разноцветным и однотонным, тканевым, резиновым или нетканым и т.д.»
- Задачи на умение проводить классификации
А) «Найди ошибки и их прокомментируй»
Например: треугольник, круг, прямоугольник, квадрат – это многоугольники.
Комментарий: примерные вопросы учителя:
— Что такое многоугольник? Какие их отличительные признаки?
— Что из перечисленных объектов можно отнести к многоугольникам? Почему?
— Что осталось? (круг)
— Почему эту фигуру нельзя отнести к многоугольникам?
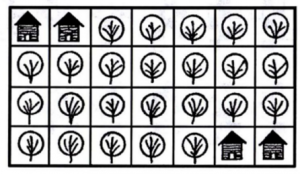
Б) Раздели этот прямоугольник на 4 одинаковых по форме части так, чтобы в каждой из них было по 1 домику и по 6 деревьев.
Комментарий:
— Что обязательно должно составлять одну целую часть? (6 деревьев и 1 домик)
— Сколько домиков вы видите на картинке? (4)
— Значит сколько должно получиться всего частей? (4)
— В какой области картинки будет лучше начать искать часть (в центре, с края)?
— Лучше начинать с края, рассмотрим верхний левый крайний домик и деревья, примыкающие к нему.
По аналогии дети делают с другого края, затем вместе с учителем выясняют, что крайние части расположены в противоположных направлениях. Аналогично поработать с оставшимися двумя частями.
- Задачи на умение сравнивать объекты
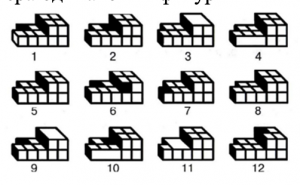
Задача: напиши номера одинаковых фигур
Комментарий: детям нужно найти сначала более схожие, на первый взгляд, фигуры, различия которых не бросаются в глаза, а затем искать уже более мелкие отличия, не сразу заметные.
— Какие фигуры, на ваш взгляд, практически одинаковые? Назовите номера. (называют с ошибкой)
— А теперь присмотритесь, и скажите, уверены ли вы в этом? Давайте проверим вместе (выясняется ошибка).
— Теперь посмотрите внимательнее на элементы фигур и найдите полностью одинаковые.
Дети находят, и выясняется, что мы не всегда замечаем отличия схожих, на первый взгляд, объектов, а также своих ошибок, поэтому нужно всегда внимательно проверять себя.
- Задачи на выявление закономерностей
Задача: найдите закономерность и вставьте пропущенные буквы и цифры:
875 – 739 яблоко – бок
902 – 898 карета – карта
434 – 389 детали – ?
561 – ? скатерть – катер
Комментарий:
— Как вы думаете, зачем здесь числовые выражения в левом столбике?
— Посчитайте, сколько букв в каждом слове в правом столбике.
— Что можете сказать теперь?
— Посчитайте первые 2 примера и объясните связь полученного числа со словами, расположенными справа.
Решение:
875 – 739 = 136. Если в слове «яблоко» убрать 1,3,6 буквы, то получится слово «бок». Проверим найденную закономерность на втором примере.
902 – 898 = 4. Если в слове «карета» убрать четвёртую букву, то получится слово «карта». Применим найденную закономерность к третьему заданию.
434 – 389 = 45. Убираем четвёртую и пятую буквы в слове «детали», получаем «дети».
Слово «катер» получается из слова «скатерть», если в нём убрать 1,7 и 8 буквы. Это означает, что разность чисел равна 178. Найдём вычитаемое. Для этого из уменьшаемого вычтем разность: 561 – 178 = 283.
Ответ: дети, 283.
- На умение экспериментировать
Задача: переложи одну спичку из одного числового равенства в другое так, чтобы оба равенства стали верными.
Ответ: нужно спичку из второго равенства из числа 11 переставить перед числом 11 в первом равенстве
Комментарий: детям предлагается методом проб и ошибок найти верное решение задачи. Перекладывать спичку до тех пор, пока равенство не станет верным.
Вопросы учителя:
— Прочитайте равенства, которые перед вами. Что вы можете сказать? (ошибка в первом примере)
— Посчитайте правую часть равенства в первом примере. Сколько получается? (19)
Значит слева от знака «равно» какое должно стоять число? (19) Как оно обозначается римскими цифрами?
— Теперь посмотрите на 2-й пример. Правильно ли составлено выражение? (нет)
— Как исправить, чтобы оба примера стали верными? (нужно спичку из второго равенства из числа 11 переставить перед числом 11 в первом равенстве).
- На умение формулировать суждения
Задача.
Миша решает задание: сравните выражения 36-7 … 36-4.
В ответе он написал: «так как 7>4, то 36-7<36-4». Объясните ответ Миши.
Ответ: Миша рассуждал так: чем больше вычитаемое, тем меньше будет число, соответственно, чем меньше вычитаемое, тем число больше. С левой стороны неравенства из 36 вычитают большее число по сравнению с правой стороной неравенства, а значит слева число будет меньше, чем справа.
Комментарий:
— Можно ли решить неравенство, не вычисляя выражения?
— Если я заберу у кого-нибудь из вас пенал, тетрадь и дневник, что останется? (допустим, только учебник) Сколько предметов я забрала? А сколько осталось?
— А если я возьму только пенал, что тогда? (останется 3 предмета)
— получается, что чем больше я забираю, тем меньше у вас остаётся и наоборот.
— Вернемся к выражению. Как рассуждал Миша? Рассуждения Миши похожи на мои?
— Сформулируйте утверждение на примере компонентов разности.
- На составление причинно-следственных связей
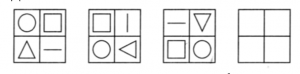
Задача: назовите четыре геометрические фигуры, размещённые внутри каждого квадрата. Проследите за тем, как изменяется расположение четырёх фигур в первых трёх квадратах. Заполните пустые клетки. Объясните, на основании чего вы это сделали.
Назовите причину изменения расположения фигур в квадрате.
Ответ: фигуры перемещаются по кругу, в левую сторону, переворачиваясь против часовой стрелки вокруг самих себя.
Комментарий: здесь дети должны увидеть закономерность перемещения фигур и выяснить, почему они изменяют свое положение таким образом, то есть установить причину увиденного следствия.
Вопросы учителя:
— Какие фигуры изменяют свое положение? (линия и треугольник)
— А какие кажутся везде одинаковыми? (круг и квадрат)
— Какие изменения происходят в каждом квадрате? (фигуры перемещаются против часовой стрелки внутри делений квадрата)
— Как вы это поняли?
— А что происходит с самими фигурами? (вращаются вкруг себя)
Можно ввести в заблуждение, задав вопрос: а все ли фигуры вращаются вокруг себя?
Дети могут ответить нет, в случае чего спросить: «почему вы так считаете? А почему вы исключили круг и квадрат?» (на рисунке мы можем только мысленно представить, что они вращаются, так как их внешние признаки не позволяют об этом узнать).
- На умение работать с текстом
Задача: летели утки. Одна спереди, две позади, одна позади и две спереди, одна между двумя и три в ряд. Сколько всего летело уток?
Решение: изобразим схематически, как летели утки:
Как видно из рисунка, речь в задаче идёт о трёх утках
Ответ: 3 утки
Комментарий: учащиеся должны научиться правильно работать с текстом. В этом задании предлагается изобразить в виде схемы/рисунка условие, чтобы тем самым структурировать информацию и сделать её более доступной для восприятия.
- На умение доказывать правильность точки зрения.
Задача: как изменится площадь прямоугольника, если одну его сторону увеличить на 3 см, а другую – уменьшить на 3 см?
Ответ: площадь может увеличиться, уменьшиться или остаться прежней.
Комментарий: для решения задания нужно рассмотреть возможные исходы события.
Учитель спрашивает, задаёт наводящие вопросы:
— Как вы считаете, площадь фигуры изменится?
— А как вообще может измениться площадь фигуры?
— То есть если в этой задаче не однозначный ответ, то может возникнуть только 3-и варианта. А если площадь все-таки меняется? Как это проверить?
— Давайте нарисуем прямоугольник. Каждый в своей тетради изобразит прямоугольник, изменит длины сторон, а затем мы сравним результаты.
— Какие же ответы у нас получились?
— То есть получается, что мы имеем 3-и решения задачи, но и возможных вариантов ответов тоже 3-и, а значит, что ответ к нашей задаче: площадь может уменьшиться, не измениться или увеличится.
В представленном примере ученикам предлагается самостоятельно исследовать проблему, связанную с изменением площади прямоугольника. Учитель вызывает у учеников сомнение, помогает сформулировать предположение, интерпретировать полученные результаты.
Подобрав разные длины сторон прямоугольников, учащиеся заметят, что показатели площадей меняются. Следовательно, нужно доказать, что однозначного ответа на вопрос задачи не существует, и найдутся такие примеры прямоугольников, что при изменении длин их сторон, площади прямоугольников будут либо увеличиваться, либо уменьшаться, либо останутся прежними.
Таким образом, представленная нами методика может быть эффективна в учебном процессе. Она показывает, что исследовательская деятельность осуществима не только во внеурочной деятельности, но и в рамках отдельных дисциплин. Конечно, мы понимаем, что существует классический подход по формированию исследовательских умений, но, как мы видим, составленная система задач, последовательно применяемая на уроках математики, соответствует всем этапам исследовательской работы. Деятельность по данному предмету – целенаправленное средство развития учащихся, стимулирования у них познавательной и творческой активности, формирования логического мышления и учебной самостоятельности. Однако, результат будет заметен только после систематических, регулярных, комплексных занятий.
Список литературы.
- Матвеева, В. А. Метод заблуждений в обучении математике / В. А. Матвеева, Н. А. Самсикова // Преподаватель XXI век. – 2022. – № 3-1. – С. 122-128.
- Романова, М. А. Решение нестандартных задач с помощью графических моделей / М. А. Романова, А. А. Вендина // Начальная школа. – 2022. – № 3. – С. 18-21.
- Савенков, А.И. Психологические основы исследовательского подхода к обучению / А.И. Савенков. – М.: Просвещение, 2006. – 434 с.
- Холодова О.А. Юным умникам и умницам: Задания по развитию познавательных способностей (9 – 10 лет): Рабочие тетради: В 2-х частях, часть 2 / О.А. Холодова. – 3-е изд. – М.: Издательство РОСТ. – 64 с.
http://izvestia-ippo.ru/matveeva-v-a-golubkova-d-a-rabota-s-tek/