магистрант ИЦО ГАОУ ВО МГПУ, Москва
denislyutts@rambler.ru
Статья посвящена использованию графического калькулятора Desmos Graphing Calculator на уроках математики. Приведен отбор математических функций, с помощью которых можно наглядно показать обучающимся, как можно использовать данную программу для совершенствования навыков моделирования.
Все естественные и общественные науки, использующие математический аппарат, занимаются математическим моделированием: заменяют реальный объект его моделью и затем изучают последнюю. Именно математика в данном вопросе является главенствующей наукой, основная цель которой – изучение реальных ситуаций с помощью математических моделей. Математика изучает реальные ситуации, а первичная математическая модель – функция, поэтому функции, их свойства и графики, как в явной, так и в неявной форме составляют стержень школьного курса математики.
В наше время большинство школ Российской Федерации имеют в своем оснащении достаточное количество современной техники, такой как персональные компьютеры, мультимедийные проекторы и графические доски, что позволяет использовать на уроках все возможности современных информационно коммуникационных технологий при обучении математике [2].
Отметим, что в структуре единого государственного экзамена (ЕГЭ) по профильной математике превалируют задачи, связанные с исследованием функций. В задаче ЕГЭ №6 идет проверка знаний обучающихся связанных с понятием производной и касательной функции в точке [4, 5].
Задача ЕГЭ №11 посвящена вопросам, связанным с точками экстремума функций. Хотя и не подразумевается конкретное построение графиков, но без фундаментального понимания, как себя ведет та или иная функция в зависимости от знака производной и что собой представляют точки максимума и минимума, невозможно осознанное выполнение данной задачи. Отдельно стоит задача ЕГЭ с параметром № 17, в которой зачастую приходится прибегать именно к графическому решению с последующим исследованием полученной функции и нахождению точек экстремума [3].
Очевиден тот факт, что полноценное и качественное обучение математики на современном этапе развития педагогики в нашей стране невозможно без использования современных компьютерных программ, интегрированных на уроках различными способами [1]. С помощью Desmos Graphing Calculator можно проводить не только построение всевозможных графиков, но и находить решения различных уравнений графическим способом с большой точностью [5]; исследовать графики производных функций первого и второго порядков.
Данная программа применяется в старших классах на уроках алгебры при подготовке к сдаче ЕГЭ по профильной математике. Обучающиеся сталкиваются со сложными функциями, которые они могут исследовать с помощью аппарата алгебры (найти производные, значение функции в точках максимума и минимума), но построение самой функции может отнять очень много драгоценного времени урока. Графический калькулятор Desmos поможет быстро и качественно построить необходимый график функции, выделить точки пересечения с осями координат, точки максимума и минимума.
Рассмотрим одну из самых популярных задач на оптимизацию из ЕГЭ. И составим математическую модель ее решения [3].
Задача 1. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Решение. Отправим на первый объект человек, их зарплата составит На второй объект отправим человек и им заплатим Всего придется заплатить
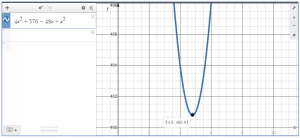
Полученная функция будет являться математической моделью данной задачи, то есть, показывать, сколько будет стоить труд рабочих. Как в любом производстве, мы всегда стремимся минимизировать расходы, найдем, при каких значение данной функции будет наименьшее. Построим данный график в среде Desmos (рисунок 1). В автоматическом режиме определилась точка минимума функции, а именно: точка . Но ведь мы не можем отправить на первый объект работать человека, поэтому необходимо найти значение функции в ближайших целых точках и сравнить их.
Ответ. На первый объект отправим работать 5 человек, а на второй оставшиеся 19 человек.
Можно было решить эту задачу и алгебраически, используя аппарат производной, но тогда не было бы такого уровня наглядности, который обеспечивается построением графиков в программе Desmos. Помимо этого идет развитие умений моделирования у обучающихся на более высоком уровне, так как полученный результат можно увидеть наглядно, оценить полученные данные с помощью построенного графика.
Рис. 1. Задача 1
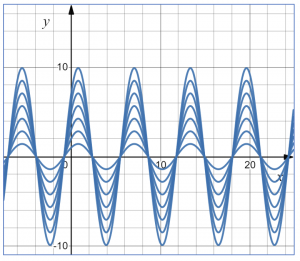
Задача 2 (практико-ориентированная задача). Институтом космических исследований РАН был зарегистрирован внеземной сигнал с частотой, описываемой функцией , где коэффициент является целым числом и зависит от дня недели, в котором был зарегистрирован сигнал. Постройте модель данной задачи и найдите наибольшее и наименьшее значения функции.
Целесообразно построить один-два графика в тетради (при ), а дальнейшее построение функции в зависимости от изменения параметра можно рассматривать с помощью программы Desmos. Удобство данной программы заключается не только в быстром и качественном построении всевозможных графиков, но и большим набором встроенных инструментов, таких как изменение цвета, ширины линии, выбор определенного интервала для параметра и многое другое, что позволяет на более высоком уровне исследовать и изучить тот или иной график. Пример построения графика функции с изменением параметра на отрезке представлен на рисунке 2.
Рис. 2. Внеземной сигнал
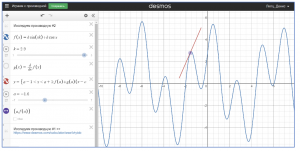
Приведем еще один пример с исследованием графика производной функции. Заметим, что в программе Desmos мы можем строить графики функций, задавая значения параметра на некотором промежутке, как на рисунке 3.
Рис. 3. Исследование графика производной
Можно сделать вывод о том, что применение программы Desmos способствует развитию умений моделирования на уроках математики, повышению наглядности на уроке. У обучающихся появляется большая мотивация изучать математику, а также работать с исследованием графиков в домашних условиях, так как программа интуитивно простая и является абсолютно бесплатной. Появляется возможность построения и исследования графиков функций задач ЕГЭ повышенного уровня (17 задача с параметром).
Учитывая активное участие общественности (учителя математики, физики и др.) в развитии дополнительных материалов к данной программе, в том числе и математических игр для средней школы, можно с большой уверенностью говорить о том, что данная программа будет использоваться гораздо чаще, чем какие-либо другие на уроках математики в ближайшем будущем.
Литература
- Глизбург В.И. Математическая обработка информации. Монография. М.: Издательство «Перо», 2020. — 162 с.
- Глизбург В.И. Цифровые ресурсы в образовательном процессе. В сб. трудов Международной научно-практической конференции преподавателей, аспирантов, студентов «Начальное филологическое образование и подготовка учителя в условиях цифровизации», Москва, МГПУ, 2021. — С. 58-61.
- Контрольно-измерительные материалы (КИМ) ЕГЭ. Режим доступа: http://fipi.ru/sites/default/files/document/2015-2019/variant/maprof_101.pdf (дата обращения: 06.11.2021).
- Приказ № 632 Министерство просвещения Российской Федерации [Электронный ресурс]. URL: https://docs.edu.gov.ru/document/444714232 cf3aff28e7b363309aa7fcb/ (дата обращения: 06.11.2021).
- Desmos [Электронный ресурс]. URL: https://www.desmos.com/?lang=ru (дата обращения: 06.11.2021).
http://izvestia-ippo.ru/lyutc-d-a-formirovanie-umeniy-modeliro/