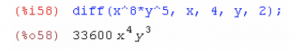Лютц Д.А. | ФОРМИРОВАНИЕ У ОБУЧАЮЩИХСЯ СТАРШЕЙ ПРОФИЛЬНОЙ ШКОЛЫ УМЕНИЙ МОДЕЛИРОВАНИЯ

магистрант ИЦО ГАОУ ВО МГПУ, Москва

denislyutts@rambler.ru

Проводить построение математических моделей к задачам является одним из основополагающих аспектов при обучении учащихся математике. В рамках данной статьи будет определено место моделирования при обучении приложениям производной функции, а также выявлены основные шаги для формирования умений моделирования у обучающихся старшей профильной школы.

Сегодня учащиеся профильной школы хотят обладать умениями и знаниями, которые можно будет применить в их дальнейшей профессиональной деятельности. К их подготовке предъявляются более высокие требования, тем самым учащиеся профильной школы всё чаще обучаются с помощью новых технологий, дающих им возможность плодотворного повышения уровня математических знаний [8]. Профилизация образования сегодня взаимосвязана с повышающимися требованиями к качеству образования[3,4].

В рамках обучения учащихся профильной школы и формирования у них умений анализировать различного рода задачи сегодня активно используется метод математического моделирования. Данный метод довольно успешно применяется при упрощении и решении практико-ориентированных задач. Перед учащимися ставится проблемная ситуация, в которой необходимо проанализировать исходные данные и построить математическую модель для поиска наиболее точного решения.

В данном случае учащиеся максимально приближают свои знания и математические навыки к анализу реальных ситуаций, составлению математических моделей.

Можно сказать, что решение задач с помощью моделирования приучает обучающихся сопоставлять данные, выделять наиболее важные аспекты, а также находить особенное в самых привычных действиях, упрощать процесс понимания сути задачи [2].

Различные современные, интерактивные и технологичные способы формирования у обучающихся математических умений отражены в действующих программах обучения. Однако, сегодня педагоги по-прежнему пытаются найти всё более успешные способы повышения мотивации у учеников при моделировании различных процессов из окружающего нас мира. И так как большинство процессов можно описать с помощью некоторых функций, то на помощь приходит именно аппарат производной функции, который как раз активно изучается в старших классах.

В целом, решение задач с помощью математического моделирования является процессом помощи учащимся в усвоении разных теорий, развития у них способностей применять полученные знания в реальной жизни.

Предъявляемые требования к процессу формирования у учащихся различных математических умений возрастают. Обучающийся старшей профильной школы сегодня стремится быть интеллектуально развитой личностью, мотивированной на плодотворное разрешение задач в жизни [3].

Умение математического моделирования является интегративным качеством, которое можно использовать не только при решении математических задач, но и применять в смежных предметных областях.

Главной целью реализации формирования у учащихся старшей профильной школы умений математического моделирования, является овладение ими различными способами моделирования (график, чертеж, запись с помощью математических символов) [5].

Методика формирования у обучающихся подобных умений отражается в следующих этапах, взаимосвязанных между собой:

— реализация получения учащимися понимания значения моделей в рамках нового материала;

— формирование представлений и выявления роли математических моделей в процессе разрешения задач;

— изучение математических моделей и их функций, необходимых для решения задач;

— реализация решения задач, в частности, связанных с приложениями производной функции;

— выявление проблемных вопросов и сложностей при решении задач, связанных с приложениями производной функции, при применении математических моделей;

— решение задач, связанных с приложениями производной функции, применяя математические модели;

— закрепление знаний и умений с помощью решения отдельных практических упражнений и задач.

По ходу осуществления обучения учащиеся должны овладеть следующими умениями:

— правильно читать графики функций;

— уметь изображать графики различных функций, например:

Так как полученные уравнения при решении различных задач порой бывают достаточно сложными, например, , то в современном мире создание математических моделей идет бок о бок с использованием различных языков программирования для более быстрого и качественного анализа полученных функций [4].

В таблице отражены этапы реализации методики по формированию у учащихся профильной школы умений моделирования при обучении приложениям производной функции с использованием современных языков программирования.

Таблица – Основные этапы реализации методики

Этапы создания умения	Задания, реализующие этапы создания умения	Демонстрационные и динамические инструменты визуализации этапа
1. Мотивация учащихся на плодотворное изучение математических моделей и их применения с использованием Maxima	Подбор заданий на изучение понятий и теорем	Показ проблемной ситуации при решении задач с использованием производной функции, побуждающей строить математические модели с использованием программы Maxima
2. Выделение функций и свойств моделирования для изучения приложений производных функций	Решение задач и упражнений на построение различных моделей.	Осуществление учащимися решения заданий по динамическим или готовым конструкциям при определении и нахождении производной функции
3. Активный процесс реализации применения математического моделирования в процессе решения задач, связанных с нахождением производных.	Ознакомление с теоремами и сопутствующими материалами, программой Maxima, помогающей реализовывать математическое моделирование	Построение математической модели.

 

Рассмотрим пример, когда учащиеся знакомятся с установкой и интерфейсами программы Maxima. Здесь у них формируются умения реализации графических возможностей.

Пример: найти первую производную функции y(x)=exp(x) /x^2. В данном случае, учащиеся изначально вводят функцию: y(x):=exp(x)/x^2, находят её производную согласно переменной х. Для этого вводят команду: diff(y(x),x,1); или diff(y(x),x);. В случае первой производной ее порядок можно не указывать (рисунок 1).

Рисунок 1 – Отображение функции согласно команде

При вычислении отдельных кратных производных по нескольким переменным после указания функции перечисляются переменные дифференцирования с указанием соответствующих кратностей, например, diff(x^8*y^5, x, 4, y, 2).

Рисунок 2 – Выделение переменных и нахождение кратностей функции

С помощью данной программы обучающиеся также изучают возможности построения разного рода графиков:

— явных;

— неявных;

— параметрических;

— двухмерных и трехмерных[6].

В ходе изучения приложений производной функции и разрешения задач учащиеся согласно приведенной методике реализуют следующие действия:

— вычисляют производные с помощью использования программы Maxima (например: Найти наибольшее и наименьшее значения функции f(x) = – x^2 на отрезке [–3, 1]);

— изучают производную по разного рода направлениям, дивергенции и градиенту (Найти поток векторного поля a через часть плоскости P, расположенной в первом октанте (образует острый угол с осью Oz), если   Px y z : 2 3 1.    2 ,   a xi yj zk);

— изучают условный экстремум (Найти условный экстремум функции   относительно уравнения связи );

— осуществляют решение текстовых задач, связанных с нахождением наименьшего и наибольшего значений функции;

— изучают модель производной Ньютона-Лейбница (Найти площадь фигуры, ограниченной линиями y = e ^{– x},     y = 0,     x = 0,     x = ln 3.);

— пользуются методом наименьших квадратов для разрешения заданных задач;

— применяют формулу Тейлора для решения задач с применением математического моделирования.

Решение подобных проблем помогает повышать результативность осуществляемого обучения, делает знания учащихся осмысленными, а также способствует плодотворному освоению математического моделирования реальных процессов [1].

В рамках методики в виде основного средства повышения уровня навыков моделирования, математической грамотности и развития вышеназванных умений используется метод математического прогнозирования с помощью разрешения задач, имеющих фактическое содержание. Обучение осуществляется по принципу “от простого к сложному”. Вначале рассматриваются тривиальные задачи и далее переходят к решению более трудных задач, построениям более сложных моделей [8].

В процессе формирования у обучающихся умений моделирования важно обращать внимание на их индивидуальные особенности, имеющийся опыт решения задач, разрешения проблемных ситуаций. В то же время педагог должен делать акцент на правильности решения задач и то, как обучающимися воспринимается метод математического моделирования в целом [7].

Можно сделать вывод о том, что процесс математического моделирования позволяет учащимся наглядно видеть возможность решения задач, связанных с приложениями производной функции, развивать свои умения интерпретировать информацию. С помощью плодотворной реализации выделенных этапов возможно постепенное и качественное формирование у учащихся старшей профильной школы умений моделирования.

 

Литература

 

1. Бабанская О. С. Метод математического моделирования в обучении учащихся решению прикладных задач// Психология и образование, №12, 2019 г. С. 66-70.
2. Васильева М. А. Комаров А. Д. Роль математического моделирования при решении задач// Студенческий научный поиск – науке и образованию 21 века. Материалы международной студенческой научно-практической конференции. Современный технический университет, 2017 г. С. 112-114.
3. Глизбург В.И. Математическая обработка информации. Монография. М.: Издательство «Перо», 2020. — 162 с.
4. Глизбург В.И. Цифровые ресурсы в образовательном процессе. В сб. трудов Международной научно-практической конференции преподавателей, аспирантов, студентов «Начальное филологическое образование и подготовка учителя в условиях цифровизации», Москва, МГПУ, 2021. — С. 58-61.
5. Карпикова М. А. Метод математического моделирования при обучении математике// Инструменты и механизмы современного инновационного развития. Сборник статей международной научно-практической конференции, 2018 г. С. 4-5.
6. Мишина А. А. Моделирование и его основные понятия, математическое моделирование// Сборник материалов международных научно-практических конференций, 2018 г. С. 429-433.
7. Никулин А. Н. Борисова Д. А. Моделирование и его основные понятия, математическое моделирование// Роль инноваций в трансформации и устойчивом развитии современной науки. Сборник статей по итогам международной научно-практической конференции, 2020 г. С. 251-254.
8. Тишина Е. М. Оптимизация процесса обучения методами математического моделирования// Современные условия взаимодействия науки и техники. Сборник статей международной научно-практической конференции, 2017 г. С. 13-17.

Annotation. The formation of mathematical models is reflected in one of the basic goals of teaching students mathematics. Within the framework of this article, the place of modeling in the field of teaching applications of a derived function will be determined, and the main steps for the formation of a methodology for creating skills of its application among students of the senior profile school will be identified.

Keywords: mathematical modeling, mathematics, derivative function.