Кдырбаева А.А., Рябова Е.В., Голиков Е. | ВЫЯВЛЕНИЕ МАТЕМАТИЧЕСКОЙ ОДАРЕННОСТИ МЛАДШИХ ШКОЛЬНИКОВ В УСЛОВИЯХ СОВРЕМЕННОГО ОБРАЗОВАНИЯ

Кдырбаева А.А.

К.ф.-м.н., профессор КазНПУ им.Абая, Алматы

E-mail: akdyrbaeva@mail.ru

Рябова Е.В.

Магистр педагогики, ст.преподаватель

КазНПУ им.Абая, Алматы

E-mail: ek_rina@rambler.ru

Голиков Е.

Студент 4 курса специальности 5В010200 –ПМНО

КазНПУ им.Абая, Алматы

 В статье рассматриваются возможности формирования и развития у младших школьников математических способностей в процессе обучения математике. Анализируется опыт работы студентов- практикантов по использованию практического материала для выявления и развития математической одаренности учащихся начальных классов.

Современный этап развития образования в республике Казахстан характеризуется обновлением целей обучения и воспитания подрастающего поколения. Это связано с социальным заказом общества, которому нужны образованные, способные, самостоятельно мыслящие, творческие личности. Для этого очень важно обнаружить таланты и способности учащихся в ходе учебного процесса и развить их. В настоящее время проводятся различные региональные, национальные и международные конкурсы, которые выявляют и поощряют высокие достижения учеников в сфере образования. Однако существует мнение, что такие конкурсные структуры не являются единственным способом развития талантов и способностей, реализации потенциала всех учеников [4, 72].

Поэтому в современной стратегии образования, направленной на развитие способностей всех его представителей, особая роль принадлежит новому учителю в широком диапазоне этого слова: воспитателю дошкольной организации, учителю школы, преподавателю колледжа, вуза, педагогу дополнительного образования. Учитель начальных классов в этом ряду призван установить индивидуальность каждого учащегося, раскрыть его талант, так как индивидуальность и одаренность — вещи взаимосвязанные [1].

Реализация этих требований   подразумевает широкий спектр педагогических приемов и методов. Специальная подготовка учителя в этой области поможет эффективно выявлять талантливых детей и создавать специальную среду для их самореализации.

В КазНПУ им. Абая такой подготовке уделяется особое внимание.  В учебный план специальности «Начальное образование» введен курс «Инновационные подходы в преподавании и учении», разработанный и читаемый в течение ряда лет старшим преподавателем Рябовой Е.В. студентам выпускного курса. В рамках изучения данной дисциплины студенты знакомятся с новыми подходами к организации педагогического процесса. Данный курс включает в себя семь модулей, в которых раскрывается необходимость введения изменений в практику преподавания и обучения; обучения педагогов и учащихся критически осмысливать свою деятельность; введения оценки обучения и оценки для обучения; использования ИКТ в учебно-воспитательном процессе; управления классом и лидерства в классе; учета возрастных особенностей; особое внимание уделяется работе с талантливыми и одаренными. [4, 71].

Идеи, приведенные в этих модулях взаимосвязаны, и рассматриваются с опорой на учебный процесс, в котором участвуют студенты во время практики. При разработке планов-конспектов уроков будущие учителя должны отобразить эти модули, показать их взаимосвязь и влияние на результативность учебного процесса. Также во время прохождения практики студенты проводили исследования по теме одного из модулей как индивидуально, так и в группах.

Проблему формирования и развития математических способностей детей — одну из наименее разработанных на сегодняшний день методических проблем обучения математике в начальных классах, рассматривал в ходе практики Голиков Евгений. В своем исследовании он опирался на то, что «одаренность – это не просто результат высоких способностей ребенка, но в первую очередь это проблема становления его личности» [7, 23].   Содержание таких понятий, как «талантливый» и «одаренный», может быть различным. Обучающиеся могут достигать более высоких уровней, чем от них ожидают в одном или более академических предметах: артистические, спортивные, музыкальные и другие таланты. При этом они могут быть одаренными в одной сфере и испытывать трудности в другой; могут быть чрезвычайно способными на одной стадии развития, но не проявлять способностей на более поздних стадиях [5, 172].

Основными методами выявления одаренных детей в работе студента были: наблюдение, общение с родителями, учащимися и учителями, тестирование, анкетирование, беседа.

Диагностику одаренности учащихся 3 класса школы — лицея № 28 г.Алматы и общение с их родителями были проведено с помощью анкетирования на основе методики Д. Хаана и М. Каффа, А.И. Савенкова [6, 230].

Математически одаренных школьников можно характеризовать следующими аспектами: способность к логическому мышлению, способность мыслить математическими символами, способность к быстрому обобщению математических объектов, отношений и действий, гибкость мыслительных процессов, стремление к ясности, простоте, экономности и рациональности решений. [2, 416].

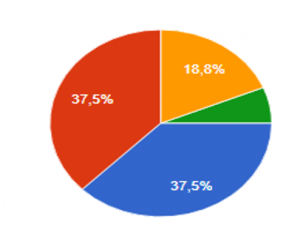
Диагностика математической одаренности учащихся 3 класса проходила в виде тестирования. На первом этапе родители учащихся ответили на 15 основных вопросов по выявлению математически одаренных детей на основе методики Савенкова А.И. [6, 231].  В тестировании участвовало 26 родителей. Опрос проводился при помощи платформы «Google Формы» (https://forms.gle/bmSYYjV7nKpWq6jc7). По итогам данного тестирования, можно сделать следующий вывод (см.диаграмму 1):

• 18,8% учащихся, самостоятельно проявляют инициативу в изучении материала с математическим уклоном.
• 6,3% учащихся являются математически одаренными детьми, которые проявляют инициативу на уроках математики и быстрее остального класса выполняют основной материал, данный на уроке.
• 37,5% учащихся, проявляют инициативу заниматься различными видами математической деятельности только под руководством взрослых, с помощью различного побуждения со стороны взрослых.
• 37,5% учащихся проявляют минимальный интерес к различной математической деятельности.

Диаграмма 1.

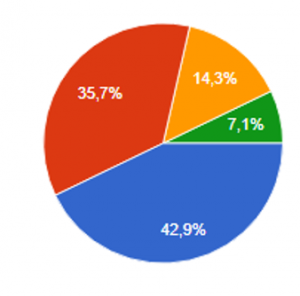
Далее родители учащихся проходили тестирования на основе методики Д. Хаана и М. Каффа [6, 230]. Тестирование состояло также из 15 вопросов по выявлению математически одаренных детей. В тестировании участвовало 26 родителей, опрос (https://forms.gle/MyEtCtEb8kF3Eprs6) проводился при помощи платформы «Google Формы» (см.диаграмму 2).

По итогам данного тестирования был сформулирован следующий вывод:

• 14,3% учащихся самостоятельно проявляют инициативу в изучении различного материала с математическим уклоном.
• 7,1% учащихся, являются математически одаренными детьми.
• 42,9% учащихся, проявляют инициативу заниматься различными видами математической деятельности. только с помощью различного побуждения со стороны взрослых.
• 35,7% учащихся, проявляют минимальный интерес к различной математической деятельности на уроках математики.

Диаграмма 2.

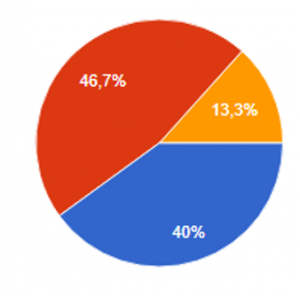
Последним этапом в процессе проведения исследования было проведено тестирование самих учащихся 3 класса, для выявления математически одаренных детей в классе [8, 130]. В тестировании участвовало 16 учащихся, опрос проводился при помощи платформы «Google Формы» (см. диаграмму 3).

По итогам данного тестирования, можно сделать следующий вывод:

• 13,3% учащихся самостоятельно проявляют интерес в развитии своих математических наклонностей, как на уроках математики, так и во внеурочное время.
• 40% учащихся, проявляют интерес к различной математический деятельности только под руководством родителей или учителя.
• 46,7% учащихся нейтрально относятся к любой математической деятельности.

Диаграмма 3.

На основании проведенного опроса можно сделать следующие выводы:

1.В данном классе присутствует 7,1% учащихся, которые проявляют максимальный интерес к различной математической деятельности, для того, чтобы продолжить развивать в учащихся математические задатки, нами был разработан ряд заданий для развития математической одаренности у учащихся и поддержки интереса одаренных учеников на уроках математики.

2. Информация, полученная от родителей и учителей ребенка, дает возможность узнать о его развитии с самых первых шагов, о наличии каких-либо способностей, интересов и т. д.

3.Реальные наблюдения в отличие от ограниченных рамок тестирования представляют информацию о поведении ребенка дома, в школе и в другом окружении.

4.Данные наблюдения помогают выявить редко встречающиеся способности, которые можно упустить в ходе тестирования ребенка. Систематическое наблюдение за ребенком позволяет составить периодизацию развития ребенка, чего нельзя сделать с помощью тестирования.

Для работы с одаренными детьми студент разрабатывал задания, которые использовал на уроке и в качестве домашних заданий. Ведь одаренным школьникам невозможно ограничиться одним учебником, готовыми решениями. Им необходимо значительное количество дополнительной литературы, заданий [3, 41].

Примеры заданий:

1. Заполни пропуски, напиши место (…) свой ответ:

1) 1 ч 28 мин = … мин

2) 3 ч 15 мин = … мин

3) 12 ч = … мин

4) 6 ч = … мин

2. Задача №1. Высокогорный спортивный комплекс Медео открыт с 1972 года. За всю свою историю он проходил две реконструкции. Первая в 2001 году, а вторая в 2008 году. Определите, какой временной промежуток прошел между открытием Медео и его последней реконструкцией. Составьте свои вопросы к задаче.
3. Задача №2. Кольсайские озёра это «жемчужина Северного Тянь-Шаня», соединяющая хребты Кунгей-Алатау и Заилийский Алатау. Популярное туристическое место Алматинской области имеет три озера, одно из озер имеет вытянутую форму с юга на север, длина водоёма 1 км, ширина до 500 м. Найдите площадь данного озера?
4. Докажи, не выполняя вычислений, что значения выражений в каждом столбике одинаковы.

9х7+9+5=            8х6+8+3=

7х9+9+5=            8х7+3=

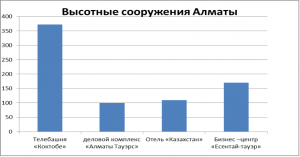
5. Используя данные диаграммы, составь задачи.

 

 Проведенное студентом исследование и работа с одаренными детьми показала, что для выявления одаренных детей нужно  осуществлять  тщательный анализ   взаимоотношений учащихся со сверстниками и другими людьми, которые  в значительной мере определяют историю его жизни и тем самым формируют его личность; для получения объективной информации необходимо проводить диагностику родителей и учителей [7, 200]; готовить учителей к работе с одаренными и талантливыми; общение с педагогом, которое является одним из важных компонентов социализации, должно строиться  на основе сотрудничества.

 

Список литературы

1. Вопросы развития математических способностей учащихся в начальной школе. Кенжебекова Р.И. — к.п.н., доцент, Казахстан г.Чимкент. http://www.rusnauka.com/13_EISN_2012/Pedagogica/3_110052.doc.htm. Дата обращения 21.12.2020.
2. Крутецкий, В.А. Психология математических способностей школьников / под ред. Н.И. Чуприковой. – М.: Изд-во МПСИ; Воронеж: МОДЭК, 1998. – 430 с.
3. Матюшкин А.М. Загадки одаренности. М.: Просвешение, 1992. – 50 с.
4. Программа дополнительного профессионального образования для студентов выпускных курсов Вузов, осуществляющих подготовку педагогических кадров, разработанная на основе уровневых программ повышения квалификации педагогических работников. Руководство для студента. -АОО «Назарбаев Интеллектуальные школы»,  2015,- 184 с.
5. Программа дополнительного профессионального образования для студентов выпускных курсов Вузов, осуществляющих подготовку педагогических кадров, разработанная на основе уровневых программ повышения квалификации педагогических работников. Руководство для тренера. -АОО «Назарбаев Интеллектуальные школы»,  2015,- 181 с.
6. Савенков А.И. Одаренные дети в детском саду и школе: Учеб. пособие для студ. высш. пед. учеб. заведений. — М.: Издательский центр «Академия», 2000 – 250 с. Автор методики / адаптация: Д. Хаан и М. Каффа / Савенков Александр Ильич.
7. Сергеева Т.Ф. Система работы с одаренными детьми: теория и практика\ Т.Ф.Сергеева, Н.А.Пронина, Е.В.Сечкарева.- Ростов н\Д: Феникс, 2011. – 284 с.
8. Шумакова Н.Б. Одаренный ребенок. Особенности обучения. Пособие для учителя. — М.: Просвещение,2008. – 145 с.

The article discusses the possibilities of formation and development of mathematical abilities in the process of teaching mathematics to younger students. The article analyzes the experience of students-interns in using practical material to identify and develop mathematical giftedness of primary school students.

Keywords: giftedness, mathematical abilities of younger schoolchildren, creative abilities, cognitive interest