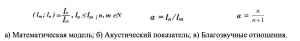Караиванова М. А.| ИЗУЧЕНИЕ МАТЕМАТИКИ – ОСНОВА ТРАНСДИСЦИПЛИНАРНОГО ИЗУЧЕНИЯ ИСКУССТВ

доктор педагогики, АМТИИ „Проф. Асен Диамандиев“, Пловдив, Болгария

E-mail: mariakaraivanova@abv.bg

Аннотация: Cтатья представляет оригинальный, трансдисциплинарный модельный подход к содержанию профилированной и общеобразовательной подготовки в школах для изучения искусств.

Такой подход применяется на основе музыкальной грамотности, приобретаемой математическими средствами. Исследованный в учебной деятельности, представленный метод показывает, что достигается баланс в развитии одарëнности и общем развитии учеников и повышается уровень их образованности.

Проблема одаренности представлена в работах Л.И. Ларионовой, А.И. Савенкова и других исследователей [4, 5, 6]. Развитие одаренных в искусстве учащихся, особенно музыкантов и художников, связывается прежде всего с совершенствованием их способностей к осознанному и целенаправленному овладению богатой палитрой эмоций. Но чувственное развитие их таланта попадает в диссонанс с тенденциями общественного развития.

Информационный кризис и технологическая экспансия перенасыщают информацией все виды человеческой деятельности и повышают в них уровень математизации и интеллектуализации. Подобная тенденция генерирует потребность в более высокой образованности, каковую одарëнные в искусствах молодые люди трудно могут приобрести. Среда для развития их таланта многократно усложняется.

1. Образовательная среда в информационном обществе. Дигитализация ставит образовательные процессы в новые условия.

Познавательные виды деятельности меняют свой характер. Мощные информационные потоки накапливают колоссальные количества разнородной информации. Всë более совершенные и широкодоступные электронные устройства обеспечивают быстрый и гибкий доступ к ней, независимо от времени и пространства. Погружëнные в электронную среду, молодые люди применяют параллельно „доцифровые“ и „цифровые“ подходы, которые взаимодействуют со скрытыми и неясными механизмами. В сознании учеников и студентов наступает интерференция традиционных и информационных подходов, а развитие их личности подвергается сильному влияниюприменения алгоритмов и электронных устройств во взаимодействии с большим объëмомразнородной информации.

Алгоритмы проявляются как надëжные познавательные „цепочки“, которые обозначают в информационном разнообразии короткий и безопасный путь к поставленной цели. Человек воспринимает их как удобную, быструю и продуктивную мысленную конструкцию для ориентации в совокупности разнородных элементов. Достаточно выполнитьзаданные правильные шаги в верной последовательности, без необходимости их осмысливать, что экономит время, и создаëт впечатление о быстром приобретении знаний. Но в алгоритмических подходах вопрос „Как?“ вытесняет вопрос „Зачем?“ и вызывает дисбаланс между продуктивным и репродуктивным мышлением в пользу последнего.

Электронные устройства позволяют быстро „обходить“ большие объëмы разнородной информации, следуя алгоритмам. Применяя их, молодые люди задерживают внимание на отдельных элементах в избранной совокупности, не задумываясь над ними. В их сознании совокупность превращается в ризому, т.е. в сеть потенциальных информационных единиц. Накапливается информированность, которая остаëтся неосмысленной, пустой и не приносит знаний.

Разнородность информации, с которой учащиеся постоянно взаимодействуют, подвергают их мышление испытанию. Развиваемое в рамках отдельных научных дисциплин, такое мышление затрудняется, не может охватить во всей целостности разнородную информацию, чтобы еë усвоить, и постепенно меняется. Оно становится репродуктивным и ризоматическим, „сетевым“. Меняется и отношение к информации: стремление к новости вытесняет рассуждения о смысле, который она несëт.

Наступает трансформация в мышлении! Линейное, логическое мышление, характерное для систематизированного научного познания, переходит в нелинейное, образное и затрудняет учащихся при овладении специализированной научной систематизацией знаний. Их „сетевое“ мышление нуждается в разнородных академических компетенциях, чтобы быть продуктивным.

Приобретаются ли такие компетенции изучающими искусства?

2. Изучение искусства в информационном обществе. Школы для изучения искусств предлагают два типа подготовки: профилированную, которая развивает и совершенствует талант, и общеобразовательную, которая гармонизирует развитие личности. Оба вида подготовки находятся в полной изоляции одна от другой – они не имеют содержательных точек соприкосновения, применяют несовместимые познавательные подходы и реализуются при дисбалансе в учебном времени, которое им предоставляется.

В своей профилированной подготовке одаренные ученики сильно мотивированы. Они увлечены овладением технологий и приёмов, с помощью которых раскрывают и совершенствуют свою чувствительность, и осознают, что степень, в которой они их постигнут, зависит от времени, которое вложат.

В то же время общеобразовательная подготовка предлагает им только отталкивающая самоцельная научность. Ученики с артистической и художественной одарëнностью принимают еë формально, как более или менее лишëнную смысла обязанность, которая обкрадывает их ценное для совершенствования в искусстве время. Одарëнные ученики достигают в своей профилированной подготовке высоких художественных результатов, но в общем образовании добиваются весьма низких академических компетенций.

Подобный дисбаланс обрекает будущих творцов на маргинализацию в обществе, для которого разносторонняя образованность приобретает исключительное значение.

Подобная неприемлемая аномалия требует, чтобы в институциях для изучения искусств вëлся поиск качественно новых познавательных подходов, совместимых с традиционными, и повысился уровень общей образованности, но не за счëт времени для развития одарëнности учеников.

3. Образовательный потенциал информационных подходов. Развитие информационных технологий опережает естественное развитие человеческого существа и предлагает ему возможности, многократно превышающие его собственные. При этих условиях формирование полноценной личности зависит от степени, в которой новые информационные подходы найдут место в образовательных процессах.

Информационный подход, как его описывает Э. П. Семенюк по А. Соколову, является анализом информационного „среза“ действительности, который раскрывает специфическую и неповторимую информационную роль каждого фрагмента из всего богатства его свойств и отношений [7, 8].

Подобный анализ в образовательном процессе перекликается с идеей трансдисциплинарности – самой современной тенденции в научном развитии, которая противопоставляется фрагментарному познанию о реальности, формирующемуся в гиперспециализации.

Трансдисциплинарность, представленная Е. О. Князевой в обоих еë проявлениях: как стратегия (по Б. Николеску) и как инженеринг, имеет методологическое значение для реализации информационных подходов в учебных видах деятельности.

Как стратегия она учитывает реальность в еë сложности, рассматривает как существующую на различных уровнях и исследует в динамике на нескольких уровнях одновременно. Трансдисциплинарные исследования допускают совмещение классической логики исключенного третьего с включением третьего и предпосылает синергетический настрой при интеграции различных дисциплин.

Как инженеринг трансдисциплинарность осуществляет перенос когнитивных схем из одной дисциплинарной области в другую с основной целью: соединить в единой картине специализированные фрагменты реальности.

В обоих случаях трансдисциплинарность поднимает существенный вопрос о правомерности, т. е. об основательности и оправданности переноса, при которой модели, разработанные и доказанные в одной области, применяются в другой, служат основанием для теоретических заключений в различных областях или им придаëтся методологическая универсальность [3].

Обеспечение правомерности находится в тесной связи с избранным „носителем“ трансдисциплинарности, т. е. научным инструментарием, который осуществляет переходы через дисциплинарные границы различных научных областей.

4. Трансдисциплинарный модельный подход в изучении искусств. Устойчивость образовательной системы требует, чтобы трансдисциплинарные информационные подходы применялись при определëнных условиях:

• Концептуально новый взгляд на образовательные стандарты учебного содержания;
• Гибкость дисциплинарных границ при научнообоснованной их проходимости;
• Совместимость новых подходов с динамикой в установленной предметной системе относительно включенных дисциплин, их тематический объëм и предусмотренное учебное время.

В таких условиях исследуется интеграция разнородного образовательного содержания, осуществляемая посредством математического моделирования. В процессе моделирования, основанном на школьной подготовке по математике, по определëнной темесинтезируютсяв органичном единстве разнородные знания и умения [1, 2].

Абстрактные по природе, математические средства трассируют переходы через дисциплинарные границы и доказывают их основательность, а оправданность переходов вытекает из тематического соединения разнородных знаний, что импонирует нелинейному мышлению, характерному для молодëжи.

Такой трансдисциплинарный модельный подход направлен на поиск баланса между общей образованностью и развитием одарëнности будущих творцов. Этот подход исследуется в учебной деятельности, раскрывая сущность древней идеи о гармонии.

Идея о гармонии синтезирована в постулате: гармония достижима, но только в единстве чувственного и рационального, и воплощена в учении   Пифагора (VI в. до н. э.). Он объединяет форму (чувственное) и количество (рациональное) в фигурное число, принимает, что мир сформирован фигурными числами и их отношениями и начинает изучать музыкальную гармония как модель всемирной гармонии. Пифагор связывает длины струны и различных еë частей с тонами, которые они издают, ис помощью трëх моделей: физической (струна), чувственной (тон) и математической (отрезок-длина), исследует различия в созвучности пар тонов.

В контексте характерной для того времени мистики, философуотдалось сформулировать правила, по которым один тон порождает ещë три тона и вместе с ними воспроизводит божественную гармонию орфеевой лиры. В современной интерпретации это открытие даëт математическое решение фундаментальной задачи в музыке: воспроизвести из тоники (Т) соответствующие ей субдоминанту (S), доминанту (D) и следующую тонику (Т^I).

Движимый идеей о единстве чувственного и рационального, Пифагор формирует основу и задаëт модель для изучения рациональным путëм музыки и еë чувственного воздействия.

Музыкальная грамотность, как самое яркое воплощение идеи о гармонии, аккумулирует знания и умения по темам изучаемых дисциплин: математика, физика, история, литература, философия, музыка, изобразительные искусства. При изучении музыки с помощью математических средств эти знания выступают в необычайных ролях и провоцируют разнородные познавательные интересы у одаренных учеников, обогащая смысловым образом их профилированную подготовку.

Идея о гармонии, раскрываемая с помощью трансдисциплинарного изучения музыки, осмысливает общеобразовательные виды учебной деятельности и приобщает к ним одарëнных молодых людей. Симбиоз „математика – музыка“ „примиряет“ изучение обеих дисциплин. Математические задачи „озвучиваются“, несовершенства музыкального слуха компенсируются количественными и структурными представлениями. Доступное каждому математическое моделирование уточняет и систематизирует построенные „по слуху“ представления о музыкальных элементах, конструкции и зависимости в них.

Приобретаемая с помощью математических средств, музыкальная грамотность положительно воздействует на познавательный процесс. В профессиональном и общекультурном плане уровень образованности повышается в значимых для будущих музыкантов и художников дисциплинах: теория музыкальных элементов, музыкальная акустика, линейные и плоскостные орнаменты, овалы, история искусств…

Числовое отношение, которым определяется понятие музыкальный интервал (Фиг.1,а), вводит количественную характеристику эстетической категории „благозвучность“ (Фиг.1,б) и раскрывает зависимость между изменениями в количественной характеристике и степени благозвучности: когда п растëт, благозвучность уменьшается.(Фиг.1,в).

Фиг. 1. Музыкальный интервал

Таким образом, эстетическая категория „благозвучие“ становится измеримой и это еë универсализирует, придаëт ей технологичность, переносимость и роль характерной особенности в творческом процессе. Посредством музыкальных отношений эти интерпретации включаются в подготовку одарëнной молодëжи.

Технологически моделируется звуковысотная организация в музыке путëм применения числовых характеристик различных благозвучий. С помощью музыкальных отношений вводятся основные музыкальныеэлементы, исследуются отношения между ними и организуются в конструкции.

Переносимость музыкальных отношений ученики опознают через их интерпретации в различных познавательных областях: изобразительное искусство, математика, архитектура… и в различные исторические периоды: Древние цивилизации, Византия, Европейское и Болгарское возрождение… [2].

Первая образная интерпретация музыкальной гармонии в Древней Греции связывается с произведением „Канон“ скульптора Поликлета (V в. до н. э.). Там он включает музыкальные отношения в своëм идеале совершенной человеческой фигуры, ведя поиск прекрасного в соотношениях целого и его частей.

Развитие математической мысли приводит к эволюции идеи о гармонии и благозвучии. Пифагор занимается поиском гармонии между двумя величинами, (Фиг.2,а), а после него неопифагорейцы (IV в. до н. э.) усложняют задачу. Они занимаются поиском третьей величины, гармоничной двум данным, (Фиг.2,б), исследуют пропорциональности и создают теорию средних величин, охваченную для изучения школьным курсом математики.

Фиг. 2. Эволюция идеи о гармонии в Древней Греции

Одаренные ученики применяют средние величины, чтобы исследовать закономерности в музыке, которые Пифагор утверждает мистикой. Устанавливают, что субдоминанта (S– кварта) является средним арифметическим обоих соседних ей тоник: Т(основнойтон) и Т^I(октава), доминанта (D– квинта) является их средней гармонической, а четыре тона орфеева строя образуют пропорцию, названную музыкальной (Фиг.2, в). Это научные доказательства о прозрении в мистических рассуждениях Пифагора.

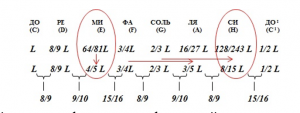
Неопифагорейцы ведут поиск совершенства в простоте числовых отношений и ревизуют сконструированную Пифагором диатоническую гамму. Упрощают отношение терции и с новым отношением изменяют сексту, септиму. Получается новая гамма (Фиг.3), в которой соседние музыкальные отношения (секунды) вписываются в обобщённую интерпретацию пифагоровой мистики. Эти отношения, как оказалось через века, входят в состав обертонового ряда, с помощью которого наука физика определяет тембр тона и даëт основание гамме неопифагорейцев быть названной натуральной.

Фиг. 3. Неопифагорейская трансформация пифагоровой диатонической гаммы

Простота натуральных музыкальных отношений утверждает их как критерии для гармонии. Интонационное богатство, которое они предлагают, приводит учащихся к другому культурному феномену: реформе в восточно-православном песнопении и личности св. Йоан Кукузела Ангелогласного, который возрожденчески сочетает церковные и фольклорные мотивы в „Полиэлей болгарки“ – „Полиелей на българката“ и „Болгарский распев“ – произведения, признанные как всемирное культурное наследие.

Стремление искать и определять благозвучность, заложенную в образ, ученики переносят в изучение математики. Находят благозвучность музыкальных отношений, связанные с определением прямого угла (египетский треугольник) или с построением центра равновесия (медицентр) в треугольнике. Исследуют изменения, которые наступают в образах геометрических форм или графиков функций при определении их параметров с помощью различных музыкальных отношений. Занимаются поиском новых функций для изучения, графики которых они находят интересными как образ.

Фиг. Математические объекты, носители благозвучности

Качество переносимости музыкальных отношений встраивают их в различные области познания и увлекает художественная сущность учеников. Они начинают выискивать скрытую благозвучность в художественных образцах, которые изучают. В образном мире Древних цивилизаций, Византии, Ренессанса и в современности ученики находят числовые отношения наиболее благозвучных музыкальных интервалов. В различные исторические периоды их благозвучие вписывается в различный контекст: мистический, религиозный, эстетический, технологический, но остаётся неизменным атрибутом гармонии.

5. Творческая интерпретация музыкальных отношений в образах. Математически выраженное благозвучие и его присутствии в художественных образцах различных культур активизирует воображение будущих художников. В их образном мышлении элементы музыкальной грамотности и математические знания, которые они приобретают, превращаются в художественные выразительные средства.

Искушëнные мыслью, что образы, которые они создают, могут „прозвучать“, ученики встраивают в них различные степени благозвучия. Показательны их разработки. Первоначально, художественная интерпретация музыкальных интервалов выражено геометрическая, затем начинает „одушевляться“ и постепенно достигает положения, в котором благозвучность порождает образы, не становясь при этом назойливой.  (Фиг. 4)

Фиг.4.Ученические художественные интерпретации

благозвучных музыкальных отношений

В процессе обучения применение музыкальных отношений совершенствуется и превращается в универсальное выразительное средство, которое служит художнику в его творческой реализации.

На основе исследования, проводившегося в школах для изучения искусств, можно утверждать:

Математическая подготовка, заложенная в этих школах, даëт возможность реализовать трансдисциплинарный модельный подход к учебному содержанию разнородных дисциплин;

Математическое моделирование, в котором устанавливаются органические связи между профилированными и общеобразовательными дисциплинами, повышают познавательную активность, расширяют круг интересов, повышают разностороннюю грамотность будущих музыкантов и художников;

Трансдисциплинарный модельный подход балансирует развитие одарëнности и общее развитие личности в соответствии с новыми общественными условиями в информационном обществе.

 

Список литературы

1. Быстрый, И.М. Школа духовно развитого человека. София: Зора, 2001, 256 -260;
2. Караиванова М. А. Трансдисциплинарный модельный подход для формирования духовности будущих художников // Психология одаренности и творчества: Сб. научных трудов II Международной научно-практической онлайн-конференции; науч. ред. чл.-корреспондента РАО, проф. А. И. Савенкова, к.псих. н., доц. В. М. Поставнев. [Электронный ресурс] – М.: 2020.
3. Князева Е. Н. Философия науки. Междисциплинарные стратегии исследований [Электронный ресурс] – М.: 2019, С.16-28.
4. Ларионова Л.И., Зверев О.М., Богданов Д.В. Особенности эмоционального интеллекта обучающихся с разными видами одареннсти (на примере ОЦ ”Сириус”) /Одарённость: условия и факторы. Материалы международной научно-практической конференции. Самара, 2029. — С.71-76.
5. Ларионова Л.И., Сафронова М.А. Имплицитные представления об интеллектуально одаренной личности/ Психология. Историко-критические обзоры и современные исследования. 2018.Т.7. 1А, С.78-82.
6. Психология одаренности и творчества / Под ред. проф. Л.И.Ларионовой, проф. А.И.Савенкова. — М.;СПб.: Нестор-История.- 2017. – 288 с.
7. Соколов А.С. Философия информации [Электронный ресурс] – М.: 2019, 61с.
8. Семенюк Э. П. Информационный подход к познанию действительности и управление // Информация и управление. – Москва, 1985. – 240 с.

Annotation. The article presents an original, transdisciplinary model approach to the content of profiled and general education training in schools for the study of the arts.

This approach is applied on the basis of musical literacy acquired by mathematical means. Investigated in educational activities, the presented method shows that a balance is achieved in the development of giftedness and the general development of students and their level of education increases.

Key words: information approach; transdisciplinarity; mathematical modeling; musical literacy.