Емельянова Е. В., Кузьмина Е. Ю., Лавлинский М. В. | Выявление структуры математических способностей у восьмиклассников

Емельянова Е. В., МБОУ гимназия №1, МАОУ лицей ИГУ, г. Иркутск

E-mail: emely07@yandex.ru

Кузьмина Е. Ю., кандидат физико-математических наук, МАОУ лицей ИГУ, г. Иркутск

E-mail: quzminov@mail.ru

Лавлинский М. В., учитель, МАОУ лицей ИГУ, г. Иркутск

E-mail: lavlinskimv@mail.ru

В статье представлено исследование особенностей структуры математических способностей восьмиклассников, обучающихся по программам профильных математического, информационного и лингвистического классов с целью подготовки лонгитюдного эксперимента. Были выделены экспериментальная (школьники, изучающие углубленно информатику), одна — контрольная (математики) и одна группа для сравнения (лингвисты, каждая группа – по 20 человек). Использована адаптированная методика с четырехкомпонентной структурой математических способностей по В.А. Крутецкому. Для краткости компоненты структуры названы: перцептивный, процессуальный, мнемонический и общий синтетический. Анализ результатов сравнения математических способностей показал, что у двух групп (математики и информатики) структурные компоненты не различаются и достоверно значимо выше уровней структурных компонент лингвистов (за исключением процессуального компонента).

The article presents a study of the structural features of the mathematical abilities of eighth-graders studying in the programs of specialized mathematical, information and linguistic classes with the aim of preparing a longitudinal experiment. An experimental group (schoolchildren studying advanced computer science), one control group (mathematics) and one group for comparison (linguists, each group of 20 people) were selected. An adapted methodology was used with a four-component structure of mathematical abilities according to V.A. Krutetsky. The components of the structure are named briefly: perceptual, procedural, mnemonic and general synthetic. Analysis of the results of comparison of mathematical abilities showed that the structural components of the two groups (mathematics and computer science) do not differ and are significantly higher than the levels of structural components of linguists (except for the procedural component).

Современная система образования нацелена на системно-деятельностный подход, который является результатом кропотливой работы целой плеяды психологов и педагогов. В частности, при исследовании таких понятий, как: обучаемость, формирование памяти, мышления, восприятия, воображения, механизмов чтения и речи, было выявлено, что ребенок развивается и развивает свои способности непосредственно в деятельности. Достоверное представление о когнитивных и личностных изменениях одаренного ребенка в образовательной среде может быть достигнуто с помощью тесного взаимодействия специалистов по психологии, педагогики, психофизиологии, информатики и математики. Учитывая современные тенденции к цифровизации школьного образования, особый интерес, по нашему мнению, представляет исследование влияния информационных технологий на специфику формирования математических способностей школьников, в частности, изменение их структурных компонентов и развитие в целом в процессе обучения.

Мы придерживались в исследовании теории математических способностей, разработанной В. А. Крутецким [5]. Ученый рассматривал структуру математических способностей с точки зрения получения, переработки и хранения математической информации. В своей модели автор рассматривает четыре структурных компонента математических способностей: «…получение математической информации, переработка математической информации, хранение математической информации, математическая направленность ума» [5, с. 345]. Мы адаптировали методику по изучению структуры математических способностей [1], отобрав отдельные серии математических задач (5 из 26) из монографии В. А. Крутецкого [5]:

— «Задачи с постепенной трансформацией из конкретного в абстрактный план» (перцептивный компонент А);

— «Задачи с постепенной трансформацией из конкретного в абстрактный план» (мнемонический компонент В);

— «Эвристические задачи», «Задачи общематематические» и «Логические задачи» (процессуальный компонент Б);

— «Задачи с различной степенью наглядности решения» (общий синтетический компонент Г).

Подробно методика описана в монографии [1]. В пять серий задач входят 45 заданий, решения которых оценивались по дихотомической шкале и переводились в проценты от общего числа заданий в каждой серии. Методика прошла апробацию на общей выборке более чем из 300 учащихся с различным уровнем математических способностей в возрасте от 11 до 18 лет [2].

В нашем исследовании были выделены 87 учащихся параллели 8-х классов с углубленным изучением математики, в частности, два класса: информационный — 30 человек и математический – 31 человек, а также один класс лингвистический — 26 человек. При дальнейшей обработке объем выборки по каждой группе был выровнен по количественному соотношению респондентов с соблюдением условия внутренней валидности по половому признаку. Таким образом, для эксперимента были отобраны 3 группы по 20 человек в каждой. Целью нашего исследования было выявить особенности структуры математических способностей учащихся информационного, математического и лингвистического профилей обучения. Первая группа – экспериментальная, вторая контрольная, последняя – для сравнения. Согласно начальной гипотезе исследования, структурные компоненты математических способностей у двух групп с углубленным изучением математики должны достоверно значимо совпадать, так как отбор учащихся для обучения в лицее ИГУ происходит на основе единых требований к уровню их подготовки как раз в 8м классе. Через два года после обучения респондентов по образовательным программам лицея различного профиля (математический, информационный, лингвистический) мы планируем повторить исследование на тех же выборках испытуемых.

Предварительный анализ сравнения двух показателей: общий уровень математических способностей (количество правильно решенных задач из батареи математических тестов) и средний балл оценок учащихся по алгебре (осреднение проводилось за два полугодия обучения в 8м классе, данные из Дневника.ру) показал высокий уровень их корреляции по Спирмену (0,530<r<0,831 при ошибке погрешности 0,017<P<0,0001). Этот факт подтверждает высокую валидность предложенной методики определять общий

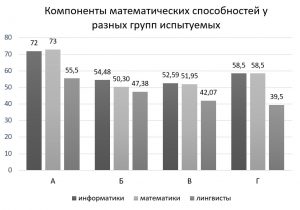
Дальнейшая обработка данных позволила выявить особенности структуры математических способностей респондентов в трех группах испытуемых. Результаты представлены на рисунке 4.

Рисунок 1. Сравнение показателей структурных компонентов математических способностей респондентов в трех группах испытуемых (компоненты: А — перцептивный, Б — процессуальный, В — мнемонический, Г – общий синтетический)

Глядя на рисунок 1, можно сказать, что перцептивный и синтетический компоненты значительно преобладают у информатиков и математиков, а все составные компоненты математических способностей лингвистов по своему уровню ниже показателей респондентов из двух других групп (математиков и информатиков). Для более точного расчета статистически значимых различий мы использовали t-критерий Стьюдента. Результаты представлены в Таблице 1.

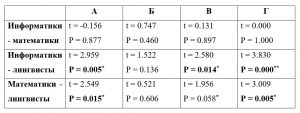
Таблица 1 – Сводная таблица значимых различий в компонентах математических способностей при попарном сравнении между показателями из трех групп респондентов

Респонденты	А	Б	В	Г
Информатики — математики	t = -0.156 P = 0.877	t = 0.747 P = 0.460	t = 0.131 P = 0.897	t = 0.000 P = 1.000
Информатики — лингвисты	t = 2.959 P = 0.005*	t = 1.522 P = 0.136	t = 2.580 P = 0.014*	t = 3.830 P = 0.000**
Математики — лингвисты	t = 2.549 P = 0.015*	t = 0.521 P = 0.606	t = 1.956 P = 0.058*	t = 3.009 P = 0.005*

Из Таблицы 1 видно, что достоверно значимых различий в показателях всех четырех структурных компонентов у математиков и информатиков не выявлено (0.460<Р<1.000). Сравнение тех же показателей между экспериментальной и контрольной группами (информатики и математики) с третьей группой (лингвисты) показали статистически значимые различия сразу у трех структурных компонентов: А – перцептивный (0.005<Р<0.015), В – мнемонический (0.014<Р<0.058), и Г – общий синтетический(0.000<Р<0.005). Процессуальный компонент Б, отвечающий за переработку математической информации у всех трех групп испытуемых, оказался почти на одном уровне.

Согласно начальной гипотезе исследования, структурные компоненты математических способностей у двух групп с углубленным изучением математики должны достоверно значимо совпадать, что и было подтверждено при статистической обработке результатов исследования.

Таким образом, мы отобрали две валидные выборки респондентов: экспериментальную и контрольную группы для формирующего эксперимента, рабочую гипотезу которого можно сформулировать так же, как и в ранних наших исследованиях [3, с. 82]: «информационные технологии влияют на положительную динамику в развитии всех компонент математических способностей». В дальнейшем мы планируем изучить динамику развития математических способностей отобранных для эксперимента групп школьников. Методика получения общего показателя уровня математических способностей также актуальна для дальнейшего отбора учащихся 7-8 классов в математические классы. Изучение структуры математических способностей в динамике позволит проверить наши ранние выводы о ее особенностях у школьников, изучающих углубленно программирование [4].

Список литературы

1. Емельянова Е.В. Тест структуры математических способностей // Психология детской одаренности и творческих способностей. Иркутск: ВСГАО, 2009. С. 38-71.
2. Емельянова Е.В. Методика диагностики математических способностей школьников и их развитие в условиях обучения информационным технологиям // Ценностные основания психологии и психология ценностей: Материалы IV Сибирского психологического форума. Томск, 2011. С. 134-137.
3. Емельянова Е.В. Особенности структуры математических способностей старшеклассников информационного профиля обучения. Сибирский психологический журнал. Томск, 2014. С. 80-89.
4. Емельянова Е.В. Особенности структуры математических способностей у старшеклассников в условиях углубленного изучения информатики // Психология личности: культурно-исторический подход. Материалы XX Международных чтений памяти Л. С. Выготского. М.: Левъ, 2019. Т. 2. С. 130-135.
5. Крутецкий В.А. Психология математических способностей школьников. М.: Институт практической психологии; Воронеж: НПО МОДЕК, 1998. 416 с.